《2025年超越训练八年级数学上册人教版四川专版》

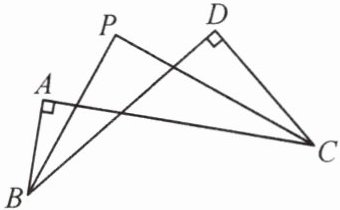
6. 如图，$ \angle A = \angle D = 90^{\circ} $，$ BP $ 平分 $ \angle ABD $，$ CP $ 平分 $ \angle ACD $，判断 $ PB $ 与 $ PC $ 的位置关系，并说明理由。

答案： 6. 解：PB⊥PC.理由如下：
∵BP平分∠ABD，CP平分∠ACD，
∴设∠ABP = ∠DBP = x，∠ACP = ∠DCP = y.
∵∠A + ∠ABD = ∠D + ∠DCA，∠A = ∠D = 90°，
∴∠ABD = ∠DCA，
即2x = 2y，
∴x = y.又∠A + ∠ABP = ∠P + ∠ACP，
∴∠A + x = ∠P + y，
∴∠P = ∠A = 90°，
∴PB⊥PC.

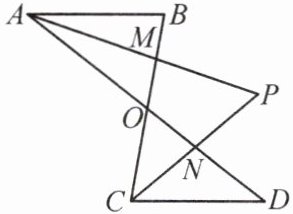
7. 如图，$ AB // CD $，$ AP $，$ CP $ 分别平分 $ \angle BAD $ 和 $ \angle BCD $，$ AD $ 与 $ BC $ 相交于点 $ O $，$ AP $ 与 $ BC $ 相交于点 $ M $，$ CP $ 与 $ AD $ 相交于点 $ N $。
(1)若 $ \angle B = 80^{\circ} $，$ \angle D = 38^{\circ} $，求 $ \angle P $ 的度数；
(2)猜想 $ \angle P $，$ \angle B $，$ \angle D $ 之间的数量关系，并说明理由。

答案： 7. 解：
(1)
∵AB//CD，
∴∠BCD = ∠B = 80°，∠BAD = ∠D = 38°，
∴∠AOC = ∠BAD + ∠B = 118°.又AP，CP分别平分∠BAD
和∠BCD，
∴$∠PAO = \frac{1}{2}∠BAD = 19°，$$∠PCO = \frac{1}{2}∠BCD =$
40°.
∵∠AOC = ∠P + ∠PAO + ∠PCO，
∴∠P = ∠AOC -
∠PAO - ∠PCO = 118° - 19° - 40° = 59°.
(2)2∠P = ∠B + ∠D.
理由如下：设∠BAM = ∠PAN = x，∠DCN = ∠PCM = y.
∵∠B + ∠BAM = ∠P + ∠PCM，即∠B + x = ∠P + y，
∴x -
y = ∠P - ∠B.
∵∠P + ∠PAN = ∠D + ∠DCN，即∠P + x =
∠D + y，
∴x - y = ∠D - ∠P，
∴∠D - ∠P = ∠P - ∠B，即
2∠P = ∠B + ∠D.

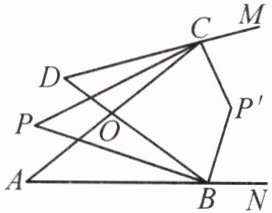
8. 如图，$ AC $，$ BD $ 相交于点 $ O $，$ BP $，$ CP $ 分别平分 $ \angle ABD $，$ \angle ACD $，$ BP' $，$ CP' $ 分别平分 $ \angle ABD $ 的邻补角 $ \angle DBN $，$ \angle ACD $ 的邻补角 $ \angle ACM $。
(1)若 $ \angle A : \angle D : \angle P = 2 : 4 : m $，求 $ m $ 的值；
(2)探索 $ \angle P' $，$ \angle A $，$ \angle D $ 之间的数量关系，并说明理由。

答案： 8. 解：
(1)
∵∠A + ∠ABP = ∠P + ∠PCA，∠D + ∠DCP = ∠P +
∠PBD，
∴∠A + ∠ABP + ∠D + ∠DCP = 2∠P + ∠PCA +
∠PBD.又BP，CP分别平分∠ABD，∠ACD，
∴∠ABP =
∠PBD，∠DCP = ∠PCA，
∴2∠P = ∠A + ∠D.设∠A = 2k，
∠D = 4k，∠P = mk，则2mk = 2k + 4k = 6k，解得m = 3.
(2)∠A + ∠D + 2∠P' = 360°.理由如下：
∵CP，CP'分别平分
∠ACD，∠ACM，
∴$∠PCP' = \frac{1}{2}(∠ACD + ∠ACM) = \frac{1}{2}×$
180° = 90°.同理可得∠PBP' = 90°，
∴∠P + ∠P' = 180°，
∴$\frac{1}{2}(∠A + ∠D) + ∠P' = 180°，$
∴∠A + ∠D + 2∠P' = 360°.