《2025年超越训练八年级数学上册人教版四川专版》

1. 如图,$AD$是$\triangle ABC$的中线,$DE$是$\triangle ACD$的中线,$EF$是$\triangle CDE$的中线,$FG$是$\triangle CEF$的中线. 若$\triangle ABC$的面积为$24$, 则$\triangle EFG$的面积为$\frac{3}{2}$.

答案： 1.$\frac{3}{2}$

2. 如图, 在$\triangle ABC$中, 延长$BC$到点$D$,$C$,$E$,$F$分别是线段$BD$,$AC$,$CD$的中点. 若$\triangle BEF$的面积为$24$, 则$\triangle ABC$的面积为32.

答案： 2.32

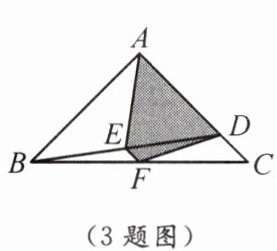
3. 如图, 在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC = 4$, 点$D$在边$AC$上,$AD = 3CD$,$E$,$F$分别是$BD$,$BC$的中点, 则四边形$AEFD$的面积为$\frac{7}{2}$.

答案： 3.$\frac{7}{2}$

4. 如图,$O$是$\triangle ABC$的重心,$BO$的延长线交$AC$于点$E$,$CO$的延长线交$AB$于点$D$. 若四边形$ADOE$的面积为$4$, 则$\triangle ABC$的面积为12.

答案： 4.12

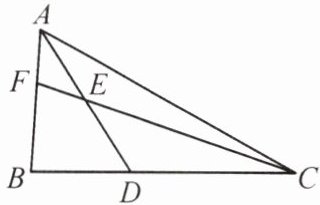
5. 如图, 在$\triangle ABC$中, 点$D$在边$BC$上, 且$BD:CD = 3:5$,$E$是$AD$的中点, 连接$CE$并延长交$AB$于点$F$, 求$\frac{S_{\triangle AEF}}{S_{\triangle CED}}$的值.

答案：
5.解:如图，连接BE.
∵BD:CD = 3:5,
∴S△BDE:S△CDE = 3:5.设S△BDE = 3x,
　　　　　　　　　　　　　　　　　　 S△CDE = 5x.
∵E是AD的中点，
∴S△ACE = S△CDE = 5x,S△ABE = S△BDE = 3x.
又$\frac{AF}{BF}=\frac{S_{\triangle ACE}}{S_{\triangle BCE}}=\frac{5x}{3x + 5x}=\frac{5}{8}$，
∴S△AEF = $\frac{5}{13}$S△ABE = $\frac{5}{13}$×3x = $\frac{15}{13}$x，
∴$\frac{S_{\triangle AEF}}{S_{\triangle CED}}=\frac{\frac{15}{13}x}{5x}=\frac{3}{13}$。