《2025年超越训练八年级数学上册人教版四川专版》

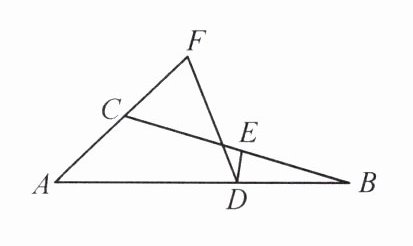
7. 如图，在$\triangle ABC$中，$D$为$AB$上一点，$\angle FDE$的两边分别交直线$AC$，$BC$于点$F$，$E$.若$AF = AD$，$BD = BE$，$\angle FDE = 30^{\circ}$，求$\angle ACB$的度数.

答案： 7.解:
∵∠FDE=30°,
∴∠FDA+∠EDB=180°−∠FDE=150°.
∵AF=AD,BD=BE,
∴∠F=∠FDA,∠EDB=∠DEB,
∴∠A+∠B=180°−2∠FDA+180°−2∠EDB=60°,
∴∠ACB=180°−(∠A+∠B)=120°.

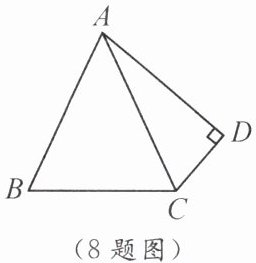
8. 如图，在四边形$ABCD$中，$AB = AC$，$CD \perp AD$.若$\angle BAC = 50^{\circ}$，$CD = \frac{1}{2}BC$，则$\angle ACD$的度数是65°.

答案： 8.65°

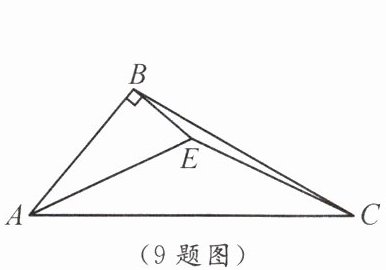
9. 如图，在$\triangle ABC$中，$AE$平分$\angle BAC$，$EB \perp AB$，$EA = EC$.若$AB = 4$，则$AC$的长为8.

答案： 9.8

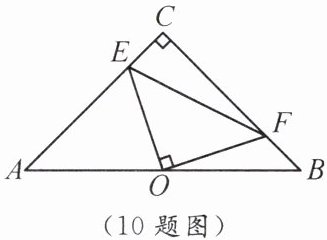
10. 如图，在$\triangle ABC$中，$AC = BC$，$\angle C = 90^{\circ}$，$O$为$AB$的中点，点$E$在$AC$上，$OF \perp OE$交$BC$于点$F$.若$AC = 4$，$CE:AE = 1:3$，则$\triangle EOF$的面积是$\frac{5}{2}$.

答案： 10.$\frac{5}{2}$

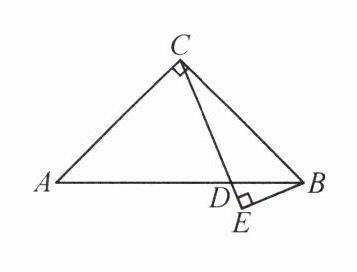
11. 如图，在等腰三角形$ABC$中，$\angle ACB = 90^{\circ}$，$AC = BC$，点$D$在$AB$上，$AD = AC$，$BE \perp CD$交$CD$的延长线于点$E$.
（1）求$\angle BCD$的度数；
（2）求证：$CD = 2BE$.

答案：
11.
(1)解:
∵∠ACB=90°,AC=BC,
∴∠A=45°.又AD=AC,
∴∠ACD=$\frac{1}{2}$(180°−∠A)=67.5°,
∴∠BCD=22.5°.
(2)证明:如图,过点A作AF⊥CD于点F.
∵AC=AD,
∴CD=2CF,∠CAF=$\frac{1}{2}$∠BAC=22.5°,
∴∠CAF=∠BCE.又∠AFC=∠CEB=90°,AC=CB,
∴△ACF≌△CBE (AAS),
∴CF=BE,
∴CD=2BE.