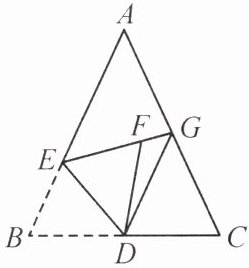
12. 如图,在$\triangle ABC$中,$AB = AC$,$\angle BAC = 50^{\circ}$,$D$为$BC$边上的中点,$E$是$AB$边上一动点,将$\triangle BDE$沿$DE$翻折至$\triangle FDE$,$EF$的延长线交$AC$于点$G$,连接$DG$.在点$E$运动过程中,$\angle EDG$的度数是否发生变化?若变化,请说明理由;若不变化,请求出$\angle EDG$的度数.

答案:
12.解:如图,连接AD.
∵AB=AC,D是BC边上的中点,
∴AD平分∠EAG.由折叠,得ED平分∠GEB,由角的平分线的性质,得GD平分∠EGC,即ED,GD是△AEG两个外角的平分线.
∵∠AEG+∠AGE=180°−∠EAG,
∴∠BEG+∠CGE=360°−180°+∠EAG,
∴∠DEG+∠DGE=$\frac{1}{2}$(∠BEG+∠CGE)=90°+$\frac{1}{2}$∠EAG,
∴∠EDG=180°−(∠DEG+∠DGE)=90°−$\frac{1}{2}$∠EAG=90°−$\frac{1}{2}$×50°=65°,即∠EDG的度数不发生变化,∠EDG的度数为65°.

12.解:如图,连接AD.
∵AB=AC,D是BC边上的中点,
∴AD平分∠EAG.由折叠,得ED平分∠GEB,由角的平分线的性质,得GD平分∠EGC,即ED,GD是△AEG两个外角的平分线.
∵∠AEG+∠AGE=180°−∠EAG,
∴∠BEG+∠CGE=360°−180°+∠EAG,
∴∠DEG+∠DGE=$\frac{1}{2}$(∠BEG+∠CGE)=90°+$\frac{1}{2}$∠EAG,
∴∠EDG=180°−(∠DEG+∠DGE)=90°−$\frac{1}{2}$∠EAG=90°−$\frac{1}{2}$×50°=65°,即∠EDG的度数不发生变化,∠EDG的度数为65°.

1. 如图,在 $\triangle ABC$ 中,$\angle B = 60^{\circ}$,$AB = 3$,$BC = 5$,$E$ 是 $BA$ 延长线上一点,点 $D$ 在 $BC$ 边上,且 $ED = EC$,$AE = 4$,则 $BD$ 的长为

2
.


答案:
1.2
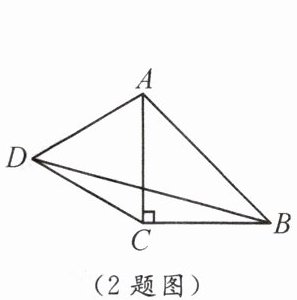
2. 如图,在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$AC = BC$,以 $AC$ 为边在其左侧作等边三角形 $ACD$,连接 $BD$.若 $AC = 4$,则 $\triangle BCD$ 的面积为
4
.
答案:
2.4
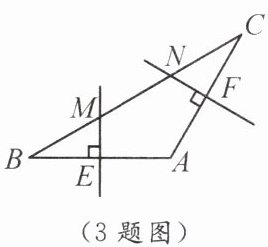
3. 如图,在 $\triangle ABC$ 中,$AB = AC$,$\angle A = 120^{\circ}$,$AB$ 的垂直平分线交 $BC$ 于点 $M$,交 $AB$ 于点 $E$,$AC$ 的垂直平分线交 $BC$ 于点 $N$,交 $AC$ 于点 $F$.若 $MN = 2$,则 $NF$ 的长为
1
.
答案:
3.1
4. 如图,$\triangle ABC$ 是等边三角形,$D$ 是 $BC$ 延长线上一点,$DE \perp AB$ 于点 $E$,$EF \perp BC$ 于点 $F$.若 $CD = 3AE$,$CF = 6$,则 $AC$ 的长为
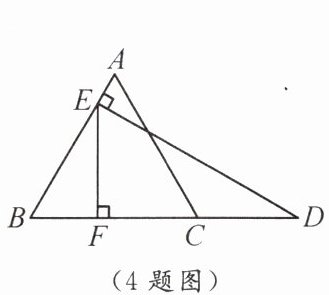
10
.


答案:
4.10
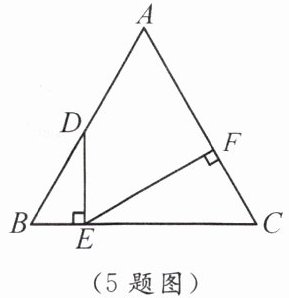
5. 如图,等边三角形 $ABC$ 的边长为 $8$,$D$ 为 $AB$ 上一动点,$DE \perp BC$ 于点 $E$,$EF \perp AC$ 于点 $F$.
(1)若 $AD = 4$,则 $AF$ 的长为
(1)若 $AD = 4$,则 $AF$ 的长为
5
;(2)当 $AD =$ $\frac{8}{3}$
时,$DE = EF$.
答案:
5.
(1)5
(2)$\frac{8}{3}$
(1)5
(2)$\frac{8}{3}$
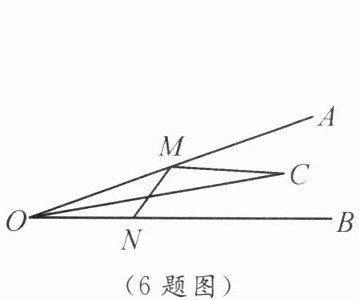
6. 如图,$\angle AOC = \angle BOC = 10^{\circ}$,$OC = 20$,$M$,$N$ 分别为 $OA$,$OB$ 上一动点,连接 $MN$,$CM$,则 $CM + MN$ 的最小值为 .
答案:
6.10
查看更多完整答案,请扫码查看


