《2025年超越训练八年级数学上册人教版四川专版》

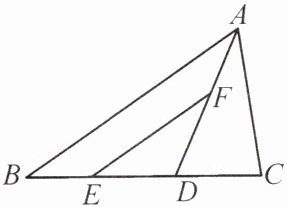
4. 如图，在△ABC 中，AD 平分∠BAC 交 BC 于点 D，点 E，F 分别在 BD，AD 上，且 DE = CD，EF//AB. 求证：EF = AC.

答案：
4.证明:如图,过点E作EM⊥AD,交AD的延长线于点M,过点C作CN⊥AD于点N.
∵∠CND=∠EMD=90°,∠CDN=∠EDM,CD=ED,
∴△CND≌△EMD(AAS),
∴CN=EM.
∵AD平分∠BAC,EF//AB,
∴∠CAN=∠BAD=∠EFM.又∠ANC=∠FME=90°,
∴△ACN≌△FEM(AAS),
∴AC=FE,即EF=AC.

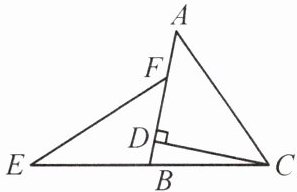
5. 如图，在△ABC 中，CD⊥AB，垂足为 D，延长 CB 至点 E，使得 EB = CB，F 是 AB 边上一点，且 FE = AC. 求证：AF = 2BD.

答案：
5.证明:如图，过点E作EG⊥AB,交AB的延长线于点G.
∵CD⊥AB,
∴∠CDB=∠G=90°.又∠CBD=∠EBG,CB=EB,
∴△CBD≌△EBG(AAS),
∴CD=EG,BD=BG.在Rt△ACD和Rt△FEG中，$\begin{cases} AC = FE \\ CD = EG \end{cases}$
∴Rt△ACD≌Rt△FEG(HL),
∴AD=FG,
∴AD−FD=FG−FD,即AF=DG=BD+BG=2BD.

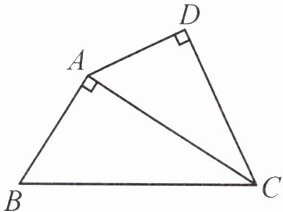
1. 如图，在四边形$ABCD$中，对角线$CA$平分$\angle BCD$，$\angle BAC=\angle D = 90^{\circ}$。若$BC = 7$，$CD = 5$，求点$B$到$AD$的距离。

答案：
1.解:如图,过点A作AM⊥BC于点M,过点B作BN⊥DA,交DA的延长线于点N.
∵CA平分∠BCD,
∴∠ACD=∠ACB.又∠D=∠AMC=90°,AC=AC,
∴△ACD≌△ACM(AAS),
∴CM=CD=5,BM=BC−CM=2.
∵∠BAC=90°,
∴∠BAN+∠CAD=90°,∠BAM+∠CAM=90°.
∵△ACD≌△ACM,
∴∠CAD=∠CAM,
∴∠BAN=∠BAM.又∠N=∠AMB=90°,AB=AB,
∴△ABN≌△ABM(AAS),
∴BN=BM=2,即点B到AD的距离为2.