《2025年通城学典课时作业本九年级物理上册苏科版苏州专版》

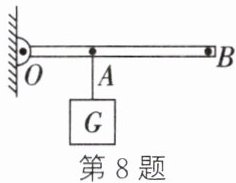
8. 如图所示,OAB为轻质杠杆,可绕支点O自由转动,在B处施加一个动力使杠杆在水平位置平衡,该杠杆(D)

A.一定是省力杠杆
B.一定是费力杠杆
C.一定是等臂杠杆
D.以上情况都有可能

答案： D

9. (2024·北京)如图,园艺工人在修剪枝条时,常把枝条尽量往剪刀的轴处靠近,这样做是为了(D)

A.增大动力臂,能够省力
B.增大阻力臂,方便使用
C.减小动力臂,方便使用
D.减小阻力臂,能够省力

答案： D

10. 如图所示,AOB为一杠杆,O为支点,杠杆自重不计,$AO= OB$。在杠杆右端A处用细绳悬挂重为G的物体,当AO段处于水平位置时,为保持杠杆平衡,需在B端施加最小的力$F_{1}$;当OB段在水平位置时,为保持杠杆平衡,这时需在B端施加最小的力$F_{2}$,则(B)
A.$F_{1}\lt F_{2}$
B.$F_{1}＞F_{2}$
C.$F_{1}= F_{2}$
D.无法比较

答案： B

11. (易错题)为了拔除外来入侵物种,农业专家自制轻质拔草器。将拔草器左下端的叉子插入植株根部,用手对拔草器施力,可将植株连根拔起。若拔同一植株,下列手施力最小的是(C)

答案： C [易错分析] 根据杠杆的平衡条件确定最小力。拔草器相当于一个杠杆，若拔同一植株，则植株对拔草器的阻力一定，由杠杆平衡条件 $F_{1}l_{1}=F_{2}l_{2}$ 可知，阻力臂越小，则动力臂越大，动力越小。A、B、C 图相比，动力臂相等，C 图中的阻力臂更小，所以 C 图动力更小。

12. 如图所示,举着哑铃的前臂骨骼可看成杠杆,画出动力$F_{1}的示意图及阻力F_{2}的力臂l_{2}$。

答案：
如图所示
　　　　　　　

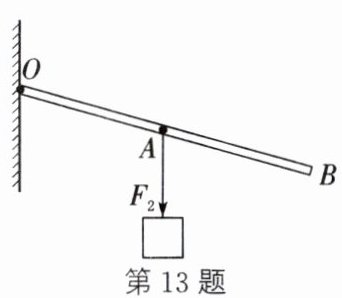
13. (2023·苏州)图中,用直棒提升重物,画出图示位置所用最小力$F_{1}和阻力F_{2}的力臂l_{2}$。

答案：
如图所示
　　　　　　

14. 如图所示,张师傅想用最省力的方法把一个油桶推上台阶。请你在图中作出杠杆的支点O、最省力的力臂l以及最小力F的方向。

答案：
如图所示
　　　　　　　

15. 如图所示是小明同学制作的杆秤的示意图,使用时将货物挂在秤钩上,用手提起B或C(相当于支点)处的秤纽,移动秤砣在秤杆上的位置,当秤杆水平平衡时,可读出货物的质量。秤砣最远可移至D点,此秤最大称量是10kg。秤杆、秤钩和秤纽的质量忽略不计,AB、BC、BD的长度如图所示,则秤砣的质量是0.4kg,提起B(B/C)处的秤纽,可以达到最大称量;如果秤砣磨损,用该秤称量的货物质量偏大(偏大/不变/偏小);距离C点12.5cm处,有两个刻度,分别为3.1kg和1kg。

答案： 0.4 B 偏大 3.1 1 解析：根据杠杆的平衡条件可知：当提着 B 处秤纽、秤砣在 D 点时，A 点所挂货物重 $G_{A}=\frac{G_{秤砣}×BD}{AB}$，当提着 C 处秤纽、秤砣在 D 点时，A 点所挂货物重 $G_{A}'=\frac{G_{秤砣}×CD}{AC}$，因 $BD＞CD$、$AB＜AC$，则 $G_{A}＞G_{A}'$，即提 B 处秤纽时，此秤的称量最大；当提着 B 处秤纽、秤砣挂在 D 点、A 点秤钩挂着质量为 10 kg 的货物时，秤杆可以在水平位置平衡，根据杠杆平衡条件可得 $G_{A}×AB=G_{秤砣}×BD$，由 $G=mg$ 可得 $m_{A}g×AB=m_{秤砣}g×BD$，则 $m_{秤砣}=\frac{m_{A}×AB}{BD}=\frac{10kg×2cm}{50cm}=0.4kg$；如果秤砣磨损，根据杠杆平衡条件可知动力臂变大，所以用该秤称量货物质量偏大；当提起 B 处秤纽时，阻力臂 $AB=2cm$，动力臂 $l_{1}=3cm+12.5cm=15.5cm$，根据杠杆的平衡条件可列式：$G_{1}×AB=G_{秤砣}×l_{1}$。由 $G=mg$ 可得 $m_{1}g×AB=m_{秤砣}g×l_{1}$，则 $m_{1}=\frac{m_{秤砣}×l_{1}}{AB}=\frac{0.4kg×15.5cm}{2cm}=3.1kg$，当提起 C 处秤纽时，阻力臂 $AC=AB+BC=2cm+3cm=5cm$，动力臂 $CD'=12.5cm$，根据杠杆的平衡条件可列式：$G_{2}×AC=G_{秤砣}×l_{1}'$。由 $G=mg$ 可得 $m_{2}g×AC=m_{秤砣}g×l_{1}'$，则 $m_{2}=\frac{m_{秤砣}×l_{1}'}{AC}=\frac{0.4kg×12.5cm}{5cm}=1kg$。