《2025年通城学典课时作业本九年级物理上册苏科版苏州专版》

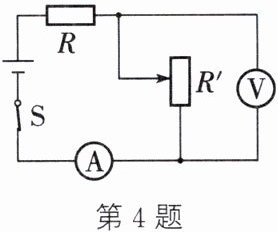
4. 如图所示,滑动变阻器$R'$的滑片在某两点间移动时,电流表的示数在1A到2A之间,电压表的示数在6V到9V之间。求定值电阻R的阻值及电源电压。

答案： $3 \, \Omega$ $12 \, \text{V}$

5. (2024·苏州工业园区校级二模)如图所示的电路中,电阻$R_{1}$的阻值为20Ω,电源电压不变,$S_{1}$、$S_{2}$断开,$S_{3}$闭合时,电流表的示数为0.6A;$S_{1}$断开,$S_{2}$、$S_{3}$闭合时,电流表的示数为0.9A。求:
(1) 电源电压及$R_{2}$的阻值。
(2) $S_{1}$闭合,$S_{2}$、$S_{3}$断开时,电阻$R_{1}$两端的电压。
(3) $S_{1}$、$S_{2}$闭合,$S_{3}$断开时,电流表的示数。

答案：
(1) 当 $S_{1}$、$S_{2}$ 断开，$S_{3}$ 闭合时，电路为 $R_{1}$ 的简单电路，电流表测电路中的电流，由 $I = \frac{U}{R}$ 可得，电源电压 $U = I_{1}R_{1} = 0.6 \, \text{A} × 20 \, \Omega = 12 \, \text{V}$；当 $S_{1}$ 断开，$S_{2}$、$S_{3}$ 闭合时，两电阻并联，电流表测干路的电流，因并联电路中各支路独立工作、互不影响，所以通过 $R_{1}$ 的电流不变，因并联电路中干路电流等于各支路电流之和，所以通过 $R_{2}$ 的电流 $I_{2} = I - I_{1} = 0.9 \, \text{A} - 0.6 \, \text{A} = 0.3 \, \text{A}$，因并联电路中各支路两端的电压相等，所以 $R_{2}$ 的阻值 $R_{2} = \frac{U}{I_{2}} = \frac{12 \, \text{V}}{0.3 \, \text{A}} = 40 \, \Omega$
(2) 当 $S_{1}$ 闭合，$S_{2}$、$S_{3}$ 断开时，两电阻串联，因串联电路中总电阻等于各分电阻之和，所以电路中的电流 $I' = \frac{U}{R_{1} + R_{2}} = \frac{12 \, \text{V}}{20 \, \Omega + 40 \, \Omega} = 0.2 \, \text{A}$，电阻 $R_{1}$ 两端的电压 $U_{1} = I'R_{1} = 0.2 \, \text{A} × 20 \, \Omega = 4 \, \text{V}$
(3) 当 $S_{1}$、$S_{2}$ 闭合，$S_{3}$ 断开时，$R_{1}$ 被短路，电路为 $R_{2}$ 的简单电路，电流表测电路中的电流，则电流表的示数 $I_{2}' = \frac{U}{R_{2}} = \frac{12 \, \text{V}}{40 \, \Omega} = 0.3 \, \text{A}$

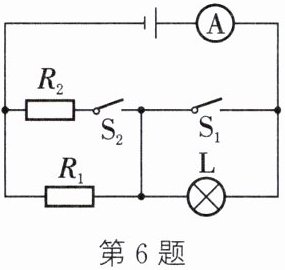
6. (2024·苏州姑苏校级段考)如图所示,$R_{1}= 25Ω$,小灯泡L的规格为“2.5V 0.3A”,电源电压保持不变。(不考虑灯丝电阻变化)
(1) $S_{1}$、$S_{2}$都断开时,小灯泡L正常发光,求电源电压。
(2) $S_{1}$、$S_{2}$都闭合时,电流表示数变为0.6A,求$R_{2}$的阻值。

答案：
(1) 由电路图可知，$S_{1}$、$S_{2}$ 都断开时，$R_{1}$ 与 $L$ 串联，小灯泡 $L$ 正常发光，所以，灯泡两端的电压 $U_{L} = 2.5 \, \text{V}$，电路电流 $I = I_{L} = 0.3 \, \text{A}$，由 $I = \frac{U}{R}$ 可得，$R_{1}$ 两端电压 $U_{1} = I_{1}R_{1} = IR_{1} = 0.3 \, \text{A} × 25 \, \Omega = 7.5 \, \text{V}$，因串联电路中总电压等于各分电压之和，所以，电源的电压 $U = U_{L} + U_{1} = 2.5 \, \text{V} + 7.5 \, \text{V} = 10 \, \text{V}$
(2) 由电路图知，$S_{1}$、$S_{2}$ 都闭合时，$R_{1}$ 与 $R_{2}$ 并联，电流表测干路电流，因并联电路中各支路两端的电压相等，所以，通过 $R_{1}$ 的电流 $I_{1}' = \frac{U}{R_{1}} = \frac{10 \, \text{V}}{25 \, \Omega} = 0.4 \, \text{A}$，因并联电路中干路电流等于各支路电流之和，所以，通过 $R_{2}$ 的电流 $I_{2} = I' - I_{1}' = 0.6 \, \text{A} - 0.4 \, \text{A} = 0.2 \, \text{A}$，则 $R_{2}$ 的阻值 $R_{2} = \frac{U}{I_{2}} = \frac{10 \, \text{V}}{0.2 \, \text{A}} = 50 \, \Omega$

7. (2024·苏州校级段考)如图所示,电源电压保持不变,电阻$R_{1}= 10Ω$,滑动变阻器$R_{2}$的最大阻值为20Ω,灯泡电阻不随温度变化。闭合开关S,当开关$S_{1}$、$S_{2}$都断开,滑动变阻器的滑片P滑动到中点时,电流表的示数为0.4A;当开关$S$、$S_{1}$、$S_{2}$都闭合,滑动变阻器的滑片P滑动到最右端时,电流表的示数为0.9A。
(1) 电源电压为多少?
(2) 灯泡的电阻是多少?

答案：
(1) 闭合开关 $S$，当开关 $S_{1}$、$S_{2}$ 都断开，滑动变阻器的滑片 $P$ 滑动到中点时，$R_{1}$ 与 $R_{2}$ 串联，电流表测电路中的电流，因串联电路中总电阻等于各分电阻之和，所以，由 $I = \frac{U}{R}$ 可得，电源电压 $U = I\left(R_{1} + \frac{R_{2}}{2}\right) = 0.4 \, \text{A} × \left(10 \, \Omega + \frac{20 \, \Omega}{2}\right) = 8 \, \text{V}$
(2) 当闭合开关 $S$、$S_{1}$、$S_{2}$ 时，灯泡 $L$ 与 $R_{2}$ 并联，电流表测干路电流，因并联电路中各支路两端的电压相等，所以，通过 $R_{2}$ 的电流 $I_{2} = \frac{U}{R_{2}} = \frac{8 \, \text{V}}{20 \, \Omega} = 0.4 \, \text{A}$，因并联电路中干路电流等于各支路电流之和，所以，通过灯泡 $L$ 的电流 $I_{L} = I' - I_{2} = 0.9 \, \text{A} - 0.4 \, \text{A} = 0.5 \, \text{A}$，则灯泡的电阻 $R_{L} = \frac{U}{I_{L}} = \frac{8 \, \text{V}}{0.5 \, \text{A}} = 16 \, \Omega$