20. 已知当m,n都是实数,且满足$2m = n + 8$时,就称点$P(m - 1,\frac{n + 2}{2})$为“爱心点”.
(1) 点$A(5,3)$,$B(4,8)$中哪个点为“爱心点”?请说明理由;
(2) 若点$M(a,2a - 1)$是“爱心点”,则点M在第
(1) 点$A(5,3)$,$B(4,8)$中哪个点为“爱心点”?请说明理由;
(2) 若点$M(a,2a - 1)$是“爱心点”,则点M在第
三
象限.
答案:
$(1)$判断点$A(5,3)$,$B(4,8)$哪个是“爱心点”
- **对于点$A(5,3)$:
已知点$P(m - 1,\frac{n + 2}{2})$,若$A(5,3)$是“爱心点”,则$\begin{cases}m - 1 = 5\\frac{n + 2}{2}=3\end{cases}$
由$m - 1 = 5$,可得$m = 6$。
由$\frac{n + 2}{2}=3$,两边同时乘以$2$得$n + 2 = 6$,解得$n = 4$。
把$m = 6$,$n = 4$代入$2m=n + 8$,左边$=2×6 = 12$,右边$=4 + 8 = 12$,左边$=$右边,所以点$A$是“爱心点”。
对于点$B(4,8)$:
若$B(4,8)$是“爱心点”,则$\begin{cases}m - 1 = 4\\frac{n + 2}{2}=8\end{cases}$
由$m - 1 = 4$,可得$m = 5$。
由$\frac{n + 2}{2}=8$,两边同时乘以$2$得$n + 2 = 16$,解得$n = 14$。
把$m = 5$,$n = 14$代入$2m=n + 8$,左边$=2×5 = 10$,右边$=14 + 8 = 22$,左边$\neq$右边,所以点$B$不是“爱心点”。
$(2)$求点$M$所在象限
因为点$M(a,2a - 1)$是“爱心点”,所以$\begin{cases}m - 1 = a\\frac{n + 2}{2}=2a-1\end{cases}$
由$m - 1 = a$,可得$m=a + 1$。
由$\frac{n + 2}{2}=2a-1$,两边同时乘以$2$得$n + 2 = 4a-2$,解得$n = 4a-4$。
把$m=a + 1$,$n = 4a-4$代入$2m=n + 8$得:
$2(a + 1)=(4a-4)+8$
去括号得$2a + 2 = 4a-4 + 8$
移项得$2a-4a=-4 + 8-2$
合并同类项得$-2a = 2$
解得$a=-1$。
则$2a-1=2×(-1)-1=-2 - 1=-3$。
所以点$M$的坐标为$(-1,-3)$,点$M$在第三象限。
综上,答案依次为:$(1)$点$A$是“爱心点”,理由见上述过程;$(2)$三。
- **对于点$A(5,3)$:
已知点$P(m - 1,\frac{n + 2}{2})$,若$A(5,3)$是“爱心点”,则$\begin{cases}m - 1 = 5\\frac{n + 2}{2}=3\end{cases}$
由$m - 1 = 5$,可得$m = 6$。
由$\frac{n + 2}{2}=3$,两边同时乘以$2$得$n + 2 = 6$,解得$n = 4$。
把$m = 6$,$n = 4$代入$2m=n + 8$,左边$=2×6 = 12$,右边$=4 + 8 = 12$,左边$=$右边,所以点$A$是“爱心点”。
对于点$B(4,8)$:
若$B(4,8)$是“爱心点”,则$\begin{cases}m - 1 = 4\\frac{n + 2}{2}=8\end{cases}$
由$m - 1 = 4$,可得$m = 5$。
由$\frac{n + 2}{2}=8$,两边同时乘以$2$得$n + 2 = 16$,解得$n = 14$。
把$m = 5$,$n = 14$代入$2m=n + 8$,左边$=2×5 = 10$,右边$=14 + 8 = 22$,左边$\neq$右边,所以点$B$不是“爱心点”。
$(2)$求点$M$所在象限
因为点$M(a,2a - 1)$是“爱心点”,所以$\begin{cases}m - 1 = a\\frac{n + 2}{2}=2a-1\end{cases}$
由$m - 1 = a$,可得$m=a + 1$。
由$\frac{n + 2}{2}=2a-1$,两边同时乘以$2$得$n + 2 = 4a-2$,解得$n = 4a-4$。
把$m=a + 1$,$n = 4a-4$代入$2m=n + 8$得:
$2(a + 1)=(4a-4)+8$
去括号得$2a + 2 = 4a-4 + 8$
移项得$2a-4a=-4 + 8-2$
合并同类项得$-2a = 2$
解得$a=-1$。
则$2a-1=2×(-1)-1=-2 - 1=-3$。
所以点$M$的坐标为$(-1,-3)$,点$M$在第三象限。
综上,答案依次为:$(1)$点$A$是“爱心点”,理由见上述过程;$(2)$三。
21. 在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点$A(2,3)$,$B(4,4)$,请在如图所示的网格区域(含边界)上按要求画整点三角形.
(1) 在图①中画一个三角形PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2) 在图②中画一个三角形PAB,使点P,B的横坐标的平方的和等于它们纵坐标的和的4倍.
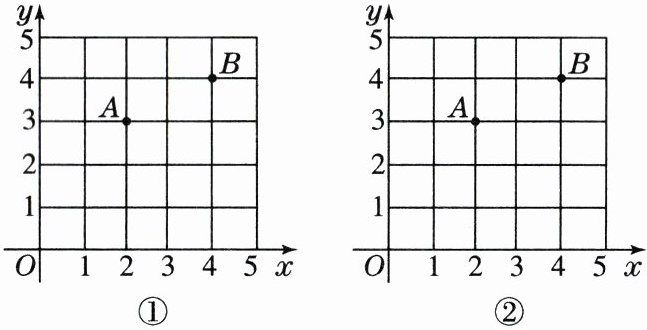
(1) 在图①中画一个三角形PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2) 在图②中画一个三角形PAB,使点P,B的横坐标的平方的和等于它们纵坐标的和的4倍.

答案:
(1) 设点$P(x, y)$,由题意知$x + y = 2$,且$x, y$均为整数。
在网格区域内,满足条件的点有$P(0, 2)$,$P(1, 1)$,$P(2, 0)$。
选择$P(0, 2)$,连接$PAB$,形成三角形$PAB$。
(答案不唯一,其他满足条件的点也可以。)
(2) 设点$P(x, y)$,由题意知$x^2 + 4^2 = 4(y + 4)$,即$x^2 + 16 = 4y + 16$,化简得$x^2 = 4y$。
在网格区域内,满足条件的点有$P(0, 0)$,$P(2, 1)$,$P(-2, 1)$,$P(4, 4)$(但$P(4,4)$与$B$重合,舍去)。
选择$P(2, 1)$,连接$PAB$,形成三角形$PAB$。
(答案不唯一,其他满足条件的点也可以。)
(1) 设点$P(x, y)$,由题意知$x + y = 2$,且$x, y$均为整数。
在网格区域内,满足条件的点有$P(0, 2)$,$P(1, 1)$,$P(2, 0)$。
选择$P(0, 2)$,连接$PAB$,形成三角形$PAB$。
(答案不唯一,其他满足条件的点也可以。)
(2) 设点$P(x, y)$,由题意知$x^2 + 4^2 = 4(y + 4)$,即$x^2 + 16 = 4y + 16$,化简得$x^2 = 4y$。
在网格区域内,满足条件的点有$P(0, 0)$,$P(2, 1)$,$P(-2, 1)$,$P(4, 4)$(但$P(4,4)$与$B$重合,舍去)。
选择$P(2, 1)$,连接$PAB$,形成三角形$PAB$。
(答案不唯一,其他满足条件的点也可以。)
22. 在平面直角坐标系中,一蚂蚁从原点O出发,依次不断移动得$A_1$,$A_2$,$A_3$,$A_4$,$A_5$,$A_6$,$A_7$,$A_8$,$A_9$,…,每次移动的距离分别为1,1,1,2,2,2,3,3,3,…,其行走路线如图所示.
(1) 填写下列各点的坐标:$A_3(-1,0)$,$A_6$(
(2) 点$A_{3n}$的坐标(n为正整数)为
(3) 求蚂蚁从原点O到点$A_{33}$移动的总路程.
(1) 填写下列各点的坐标:$A_3(-1,0)$,$A_6$(
-3
,0
),$A_9$(-6
,0
);(2) 点$A_{3n}$的坐标(n为正整数)为
$\left(-\dfrac{1}{2}n(n+1),0\right)$
;(3) 求蚂蚁从原点O到点$A_{33}$移动的总路程.
蚂蚁从原点O到点$A_{33}$移动的总路程是198.
答案:
解:
(1)$-3$;$0$;$-6$;$0$
(2)$\left(-\dfrac{1}{2}n(n+1),0\right)$
(3)蚂蚁从原点O到点$A_{33}$移动的总路程是198.
(1)$-3$;$0$;$-6$;$0$
(2)$\left(-\dfrac{1}{2}n(n+1),0\right)$
(3)蚂蚁从原点O到点$A_{33}$移动的总路程是198.
查看更多完整答案,请扫码查看


