《2025年点拨训练八年级数学上册沪科版安徽专版》

15. 在 $ \triangle ABC $ 中,$ AB = 7 $,$ BC = 2 $。
(1) 求 $ AC $ 长度的取值范围；
(2) 若 $ \triangle ABC $ 的周长为偶数,求 $ \triangle ABC $ 的周长,并判断此时 $ \triangle ABC $ 的形状。

答案： 解：
(1)5 ＜ AC ＜ 9.
(2)△ABC是等腰三角形.

16. 已知 $ y $ 与 $ x + 2 $ 成正比例,当 $ x = 4 $ 时,$ y = 12 $。
(1) 求 $ y $ 与 $ x $ 之间的函数表达式；
(2) 判断点 $ (-1,1) $ 是否在所求函数的图象上,并说明理由。

答案： $(1)$ 求$y$与$x$之间的函数表达式
- **步骤一：设函数表达式
因为$y$与$x + 2$成正比例，所以设$y = k(x + 2)$（$k\neq0$）。
- **步骤二：求$k$的值
当$x = 4$时，$y = 12$，将$x = 4$，$y = 12$代入$y = k(x + 2)$中，得到$12=k(4 + 2)$，即$12 = 6k$。
求解$k$，两边同时除以$6$，可得$k=\frac{12}{6}=2$。
- **步骤三：得出函数表达式
把$k = 2$代入$y = k(x + 2)$，得到$y = 2(x + 2)=2x + 4$。
所以$y$与$x$之间的函数表达式为$y = 2x + 4$。
$(2)$ 判断点$(-1,1)$是否在所求函数的图象上
- **步骤一：将$x=-1$代入函数表达式
把$x=-1$代入$y = 2x + 4$中，得到$y=2×(-1)+4$。
- **步骤二：计算$y$的值
根据四则运算先算乘法再算加法，$2×(-1)+4=-2 + 4=2$。
- **步骤三：判断点是否在函数图象上
因为当$x = -1$时，$y = 2\neq1$，所以点$(-1,1)$不在函数$y = 2x + 4$的图象上。
综上，答案为：$(1)$$\boldsymbol{y = 2x + 4}$；$(2)$点$(-1,1)$不在所求函数的图象上，理由：当$x = -1$时，$y=2×(-1)+4 = 2\neq1$。

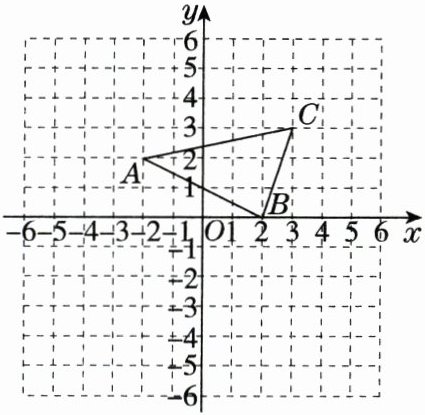
17. 如图,在平面直角坐标系中,已知 $ A(-2,2) $,$ B(2,0) $,$ C(3,3) $,$ P(m,n) $ 是 $ \triangle ABC $ 的边 $ AB $ 上的一点,把 $ \triangle ABC $ 经过平移后得到 $ \triangle DEF $,点 $ A $,$ B $,$ C $ 的对应点分别为点 $ D $,$ E $,$ F $,点 $ P $ 的对应点为 $ P_1(m - 2,n - 4) $。
(1) 直接写出 $ D $,$ E $,$ F $ 三个点的坐标并画出 $ \triangle DEF $；
(2) 求 $ \triangle DEF $ 的面积。

答案：
解：$ $　　
$(1)D,E,F$三个点分别为$D(-4,-2),E(0,-4),F(1,-1),$画图$.$　
　　　
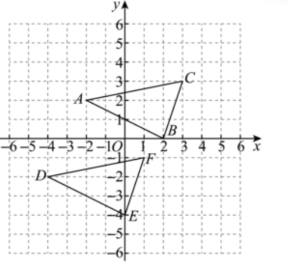
$(2)S△DEF=3×5-1/2×1×5-1/2×2×4-1/2×1×3$　　
$=15-5/2-4-3/2=7. $