《2025年点拨训练八年级数学上册沪科版安徽专版》

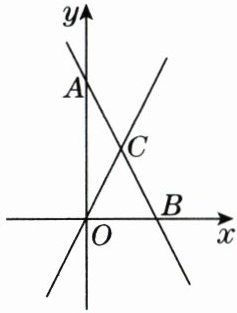
18. 如图,一次函数 $ y = ax + b $ 的图象与坐标轴交于 $ A $,$ B $ 两点,且 $ OA = 2OB = 4 $,与正比例函数 $ y = kx $ 的图象交于点 $ C $,若 $ S_{\triangle AOB} = 2S_{\triangle COB} $。
(1) 求一次函数 $ y = ax + b $ 和正比例函数 $ y = kx $ 的表达式；
(2) 结合图象直接写出不等式 $ ax + b＞kx $ 的解集。

答案： 解：
(1)一次函数的表达式为y=-2x+4,正比例函数的表达式为y=2x.
(2)由图象可得不等式ax+b ＞ kx的解集为x ＜ 1.

19. (1) 完成下面的推理说明：
已知：如图,$ BE // CF $,$ BE $,$ CF $ 分别平分 $ \angle ABC $ 和 $ \angle BCD $。
求证：$ AB // CD $。
证明：$ \because BE $,$ CF $ 分别平分 $ \angle ABC $ 和 $ \angle BCD $(已知),
$ \therefore \angle 1 = \frac{1}{2} \angle $ABC,$ \angle 2 = \frac{1}{2} \angle $BCD(角平分线的定义)。
$ \because BE // CF $(已知),
$ \therefore \angle 1 = \angle 2 $(两直线平行，内错角相等)。
$ \therefore \frac{1}{2} \angle $ABC $ = \frac{1}{2} \angle $BCD(等量代换),
$ \therefore \angle $ABC $ = \angle $BCD(等式的基本性质),
$ \therefore AB // CD $(内错角相等，两直线平行)。
(2) 说出(1)的推理中运用了哪两个互逆的真命题。
两个互逆的真命题为两直线平行，内错角相等和内错角相等，两直线平行。

答案： 解：
(1)ABC;BCD;角平分线的定义;已知;两直线平行，内错角相等;ABC;BCD;等量代换;ABC;BCD;内错角相等，两直线平行
(2)两个互逆的真命题为两直线平行，内错角相等和内错角相等，两直线平行.

20. 已知点 $ A(m,n) $ 位于平面直角坐标系中,且满足 $ 2m = 6 + n $。
(1) 若点 $ A $ 在 $ x $ 轴上,求点 $ A $ 的坐标；
(2) 已知点 $ B(3,5) $,若 $ AB // y $ 轴,求 $ m $ 的值。

答案： 解：
(1)因为点A在x轴上，所以n=0,因为2m=6+n,所以m=3,所以A(3,0).
(2)m=3.