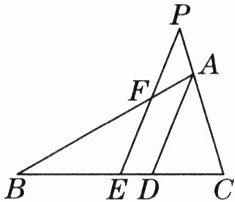
20. 如图,在 $ \triangle ABC $ 中,$ AD $ 是 $ \angle BAC $ 的平分线,$ E $ 是 $ BC $ 的中点,过点 $ E $ 作 $ EF // AD $ 交 $ CA $ 的延长线于点 $ P $,交 $ AB $ 于点 $ F $.
(1) 求证:$ \triangle APF $ 是等腰三角形;
(2) 求证:$ BF = CP $;
(3) 若 $ AB = 12 $,$ AC = 8 $,试求出 $ PA $ 的长.
(1) 求证:$ \triangle APF $ 是等腰三角形;
(2) 求证:$ BF = CP $;
(3) 若 $ AB = 12 $,$ AC = 8 $,试求出 $ PA $ 的长.

答案:
1. (1)证明$\triangle APF$是等腰三角形:
因为$AD$平分$\angle BAC$,所以$\angle BAD=\angle CAD$。
又因为$EF// AD$,所以$\angle P=\angle CAD$(两直线平行,内错角相等),$\angle AFE = \angle BAD$(两直线平行,同位角相等)。
则$\angle P=\angle AFE$。
在$\triangle APF$中,$\angle P=\angle AFE$,所以$AP = AF$(等角对等边),即$\triangle APF$是等腰三角形。
2. (2)证明$BF = CP$:
过$B$作$BG// AC$交$PE$的延长线于$G$。
因为$BG// AC$,所以$\angle G=\angle P$,$\angle GBE=\angle C$。
又因为$E$是$BC$中点,即$BE = CE$。
在$\triangle BEG$和$\triangle CEP$中,$\begin{cases}\angle G=\angle P\\\angle GBE=\angle C\\BE = CE\end{cases}$,所以$\triangle BEG\cong\triangle CEP(AAS)$。
则$BG = CP$。
因为$\angle AFE=\angle P$,$\angle G=\angle P$,$\angle AFE=\angle BFG$,所以$\angle BFG=\angle G$。
所以$BF = BG$,又因为$BG = CP$,所以$BF = CP$。
3. (3)求$PA$的长:
设$PA=x$,则$AF = x$。
因为$BF = CP$,$AB = 12$,$AC = 8$,所以$BF=12 - x$,$CP=8 + x$。
由$BF = CP$可得$12 - x=8 + x$。
移项得$2x=12 - 8$,即$2x = 4$。
解得$x = 2$,所以$PA = 2$。
综上,(1)得证$\triangle APF$是等腰三角形;(2)得证$BF = CP$;(3)$PA$的长为$2$。
因为$AD$平分$\angle BAC$,所以$\angle BAD=\angle CAD$。
又因为$EF// AD$,所以$\angle P=\angle CAD$(两直线平行,内错角相等),$\angle AFE = \angle BAD$(两直线平行,同位角相等)。
则$\angle P=\angle AFE$。
在$\triangle APF$中,$\angle P=\angle AFE$,所以$AP = AF$(等角对等边),即$\triangle APF$是等腰三角形。
2. (2)证明$BF = CP$:
过$B$作$BG// AC$交$PE$的延长线于$G$。
因为$BG// AC$,所以$\angle G=\angle P$,$\angle GBE=\angle C$。
又因为$E$是$BC$中点,即$BE = CE$。
在$\triangle BEG$和$\triangle CEP$中,$\begin{cases}\angle G=\angle P\\\angle GBE=\angle C\\BE = CE\end{cases}$,所以$\triangle BEG\cong\triangle CEP(AAS)$。
则$BG = CP$。
因为$\angle AFE=\angle P$,$\angle G=\angle P$,$\angle AFE=\angle BFG$,所以$\angle BFG=\angle G$。
所以$BF = BG$,又因为$BG = CP$,所以$BF = CP$。
3. (3)求$PA$的长:
设$PA=x$,则$AF = x$。
因为$BF = CP$,$AB = 12$,$AC = 8$,所以$BF=12 - x$,$CP=8 + x$。
由$BF = CP$可得$12 - x=8 + x$。
移项得$2x=12 - 8$,即$2x = 4$。
解得$x = 2$,所以$PA = 2$。
综上,(1)得证$\triangle APF$是等腰三角形;(2)得证$BF = CP$;(3)$PA$的长为$2$。
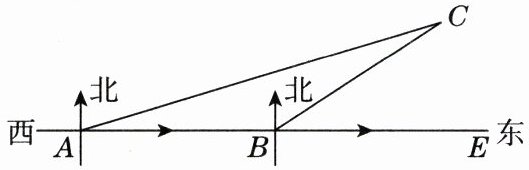
21. 如图,灯塔 $ C $ 在海岛 $ A $ 的北偏东 $ 75° $ 的方向,某天 9 时,一艘船从海岛 $ A $ 出发,以 $ 30 n mile/h $ 的速度向东航行,11 时到达 $ B $ 处,此时测得灯塔 $ C $ 在 $ B $ 处的北偏东 $ 60° $ 的方向.
(1) 求 $ \angle C $ 的度数;
(2) 已知在以灯塔 $ C $ 为中心,周围 $ 25 n mile $ 的范围内均有暗礁,若该船继续向东航行,是否有触礁的危险?请说明理由.
(1) 求 $ \angle C $ 的度数;
(2) 已知在以灯塔 $ C $ 为中心,周围 $ 25 n mile $ 的范围内均有暗礁,若该船继续向东航行,是否有触礁的危险?请说明理由.

答案:
1. (1)
首先,根据已知条件求$\angle CAB$和$\angle ABC$:
已知灯塔$C$在海岛$A$的北偏东$75^{\circ}$方向,船从$A$向东航行,则$\angle CAB = 90^{\circ}-75^{\circ}=15^{\circ}$。
灯塔$C$在$B$处的北偏东$60^{\circ}$方向,则$\angle ABE = 90^{\circ}$,$\angle ABC=90^{\circ}+60^{\circ}=150^{\circ}$。
根据三角形内角和定理$\angle A+\angle B+\angle C = 180^{\circ}$($\angle A=\angle CAB$,$\angle B = \angle ABC$)。
所以$\angle C=180^{\circ}-\angle CAB - \angle ABC$。
把$\angle CAB = 15^{\circ}$,$\angle ABC = 150^{\circ}$代入可得:$\angle C=180^{\circ}-15^{\circ}-150^{\circ}=15^{\circ}$。
2. (2)
解:过点$C$作$CD\perp AE$于点$D$。
因为$\angle CAB=\angle C = 15^{\circ}$,根据等角对等边,所以$BC = AB$。
已知船的速度$v = 30n mile/h$,航行时间$t=(11 - 9)h$,根据$s=vt$,则$AB=30×(11 - 9)=60n mile$,所以$BC = 60n mile$。
在$Rt\triangle BCD$中,$\angle CBD = 30^{\circ}$($\angle ABC = 150^{\circ}$,则$\angle DBC=180^{\circ}-\angle ABC = 30^{\circ}$)。
根据直角三角形中$30^{\circ}$所对的直角边是斜边的一半,即$CD=\frac{1}{2}BC$(在$Rt\triangle BCD$中,$\angle BDC = 90^{\circ}$,$\angle DBC = 30^{\circ}$,设$CD$为$x$,$BC$为$2x$)。
因为$BC = 60n mile$,所以$CD=\frac{1}{2}×60 = 30n mile$。
因为$30\gt25$。
所以:
(1)$\angle C$的度数是$15^{\circ}$;
(2)该船继续向东航行没有触礁的危险,因为灯塔$C$到航线$AE$的最短距离$CD = 30n mile\gt25n mile$。
首先,根据已知条件求$\angle CAB$和$\angle ABC$:
已知灯塔$C$在海岛$A$的北偏东$75^{\circ}$方向,船从$A$向东航行,则$\angle CAB = 90^{\circ}-75^{\circ}=15^{\circ}$。
灯塔$C$在$B$处的北偏东$60^{\circ}$方向,则$\angle ABE = 90^{\circ}$,$\angle ABC=90^{\circ}+60^{\circ}=150^{\circ}$。
根据三角形内角和定理$\angle A+\angle B+\angle C = 180^{\circ}$($\angle A=\angle CAB$,$\angle B = \angle ABC$)。
所以$\angle C=180^{\circ}-\angle CAB - \angle ABC$。
把$\angle CAB = 15^{\circ}$,$\angle ABC = 150^{\circ}$代入可得:$\angle C=180^{\circ}-15^{\circ}-150^{\circ}=15^{\circ}$。
2. (2)
解:过点$C$作$CD\perp AE$于点$D$。
因为$\angle CAB=\angle C = 15^{\circ}$,根据等角对等边,所以$BC = AB$。
已知船的速度$v = 30n mile/h$,航行时间$t=(11 - 9)h$,根据$s=vt$,则$AB=30×(11 - 9)=60n mile$,所以$BC = 60n mile$。
在$Rt\triangle BCD$中,$\angle CBD = 30^{\circ}$($\angle ABC = 150^{\circ}$,则$\angle DBC=180^{\circ}-\angle ABC = 30^{\circ}$)。
根据直角三角形中$30^{\circ}$所对的直角边是斜边的一半,即$CD=\frac{1}{2}BC$(在$Rt\triangle BCD$中,$\angle BDC = 90^{\circ}$,$\angle DBC = 30^{\circ}$,设$CD$为$x$,$BC$为$2x$)。
因为$BC = 60n mile$,所以$CD=\frac{1}{2}×60 = 30n mile$。
因为$30\gt25$。
所以:
(1)$\angle C$的度数是$15^{\circ}$;
(2)该船继续向东航行没有触礁的危险,因为灯塔$C$到航线$AE$的最短距离$CD = 30n mile\gt25n mile$。
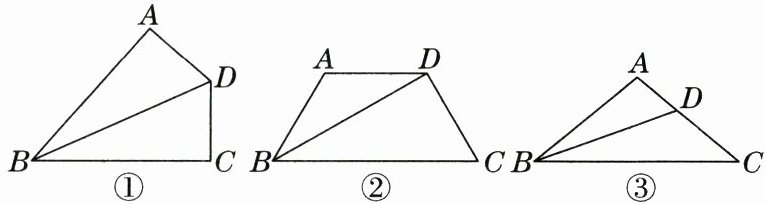
22. 我们定义:在四边形 $ ABCD $ 中,如果 $ \angle A = \alpha (0° < \alpha < 180°) $,$ \angle C = 180° - \alpha $,对角线 $ BD $ 平分 $ \angle ABC $,我们称这种四边形为“分角对补四边形”.
【特例感知】(1) 如图①,当 $ \alpha = 90° $ 时,由角平分线的性质可得 $ DA = $______;
【猜想论证】(2) 如图②,当 $ \alpha $ 为任意度数时,猜想 $ DA $ 与 $ DC $ 的数量关系,并给予证明;
【探究应用】(3) 请利用(2)中的结论解决问题:如图③,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle BAC = 100° $. $ BD $ 平分 $ \angle ABC $,求证:$ BD + AD = BC $.
【特例感知】(1) 如图①,当 $ \alpha = 90° $ 时,由角平分线的性质可得 $ DA = $______;
【猜想论证】(2) 如图②,当 $ \alpha $ 为任意度数时,猜想 $ DA $ 与 $ DC $ 的数量关系,并给予证明;
【探究应用】(3) 请利用(2)中的结论解决问题:如图③,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle BAC = 100° $. $ BD $ 平分 $ \angle ABC $,求证:$ BD + AD = BC $.

答案:
(1)DC
(2)解:DA=DC, 证明:如图①,过点D作DE⊥BA交BA的延长线于点E,DF⊥BC于点F,
∵BD平分∠EBF,DE⊥BA,DF⊥BC,
∴DE=DF.
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C.又
∵∠E=∠DFC=90°,
∴△DEA≌△DFC,
∴DA=DC.
(3)证明:如图②,在BC上截取BG=BD,连接DG,
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°.
∵BD平分∠ABC,
∴∠DBG=$\frac{1}{2}$∠ABC=20°.
∵BD=BG,
∴∠BGD=∠BDG=80°,即∠A+∠BGD=180°, 由
(2)的结论得AD=DG.
∵∠BGD=∠C+∠GDC,
∴∠GDC=∠C=40°,
∴DG=CG,
∴AD=DG=CG,
∴BD+AD=BG+CG=BC.
(1)DC
(2)解:DA=DC, 证明:如图①,过点D作DE⊥BA交BA的延长线于点E,DF⊥BC于点F,
∵BD平分∠EBF,DE⊥BA,DF⊥BC,
∴DE=DF.
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C.又
∵∠E=∠DFC=90°,
∴△DEA≌△DFC,
∴DA=DC.

(3)证明:如图②,在BC上截取BG=BD,连接DG,
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°.
∵BD平分∠ABC,
∴∠DBG=$\frac{1}{2}$∠ABC=20°.
∵BD=BG,
∴∠BGD=∠BDG=80°,即∠A+∠BGD=180°, 由
(2)的结论得AD=DG.
∵∠BGD=∠C+∠GDC,
∴∠GDC=∠C=40°,
∴DG=CG,
∴AD=DG=CG,
∴BD+AD=BG+CG=BC.
查看更多完整答案,请扫码查看


