《2025年点拨训练八年级数学上册沪科版安徽专版》

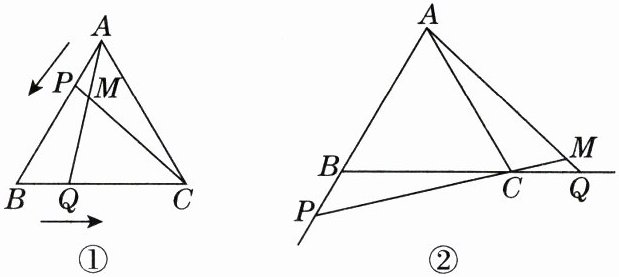
23. 如图①,已知等边三角形 $ ABC $,$ P $,$ Q $ 分别是边 $ AB $,$ BC $ 上的动点(端点除外),点 $ P $,$ Q $ 分别从顶点 $ A $,$ B $ 同时出发,向点 $ B $,$ C $ 运动,且它们的运动速度相同,$ AQ $,$ CP $ 交于点 $ M $.
(1) 求证：$ AQ = CP $；
(2) 当点 $ P $,$ Q $ 分别在 $ AB $,$ BC $ 边上运动时,$ \angle QMC $ 的大小变化吗？若变化,请说明理由；若不变,请直接写出它的度数；
(3) 如图②,若点 $ P $,$ Q $ 在运动到终点后继续在射线 $ AB $,$ BC $ 上运动,直线 $ AQ $,$ CP $ 交于点 $ M $,则 $ \angle QMC $ 的大小变化吗？若变化,请说明理由；若不变,求出它的度数.

答案： 1. （1）证明：
因为$\triangle ABC$是等边三角形，所以$AB = AC$，$\angle B=\angle CAP = 60^{\circ}$。
又因为点$P$，$Q$运动速度相同，所以$AP = BQ$。
在$\triangle ABQ$和$\triangle CAP$中，$\begin{cases}AB = AC\\\angle B=\angle CAP\\BQ = AP\end{cases}$。
根据$SAS$（边角边）定理，可得$\triangle ABQ\cong\triangle CAP$。
所以$AQ = CP$（全等三角形对应边相等）。
2. （2）
因为$\triangle ABQ\cong\triangle CAP$，所以$\angle BAQ=\angle ACP$。
因为$\angle QMC$是$\triangle ACM$的外角，根据三角形外角性质$\angle QMC=\angle ACP+\angle MAC$。
又因为$\angle BAQ+\angle MAC=\angle BAC = 60^{\circ}$，所以$\angle QMC=\angle ACP+\angle MAC=\angle BAQ+\angle MAC=\angle BAC = 60^{\circ}$。
所以$\angle QMC$的大小不变，$\angle QMC = 60^{\circ}$。
3. （3）
因为$\triangle ABC$是等边三角形，所以$AB = AC$，$\angle ABC=\angle BAC = 60^{\circ}$。
所以$\angle ABP=\angle ACQ = 120^{\circ}$。
又因为$AP = BQ$（点$P$，$Q$运动速度相同），$AB = BC$，所以$BP = CQ$。
在$\triangle ABP$和$\triangle ACQ$中，$\begin{cases}AB = AC\\\angle ABP=\angle ACQ\\BP = CQ\end{cases}$。
根据$SAS$定理，可得$\triangle ABP\cong\triangle ACQ$。
所以$\angle BAP=\angle CAQ$。
因为$\angle QMC$是$\triangle APM$的外角，根据三角形外角性质$\angle QMC=\angle P+\angle BAP$。
又因为$\angle BAP=\angle CAQ$，$\angle CAQ-\angle PAC=\angle BAC = 60^{\circ}$。
所以$\angle QMC=\angle P+\angle CAQ-\angle PAC$，而$\angle P+\angle CAQ-\angle PAC=\angle ABC = 120^{\circ}$（$\angle P$与$\angle ACB$有关系，通过外角和全等转化）。
所以$\angle QMC$的大小不变，$\angle QMC = 120^{\circ}$。
综上，（1）已证$AQ = CP$；（2）$\angle QMC$不变，为$60^{\circ}$；（3）$\angle QMC$不变，为$120^{\circ}$。