23. 综合与实践
【问题情境】数学活动课上,老师提出了如下问题:如图,在△ABC中,$AB = AC$,P是BC上一点,过点P作$PD\perp AB$,$PE\perp AC$,垂足分别为D,E,过点B作$BF\perp AC$,垂足为F,连接AP.
【特例探究】(1)如图①,当P为BC边的中点时,利用面积之间的关系可以发现线段PD,PE,BF之间的数量关系为
【深入探究】(2)如图②,当P为BC边上的任意一点时,(1)中的数量关系是否仍然成立?若成立,请加以证明;若不成立,请写出成立的数量关系,并说明理由.
【拓展探究】(3)如图③,当点P在BC边的延长线上时:
①试猜想线段PD,PE,BF之间的数量关系,并证明你的猜想;
②当$S_{\triangle ABC}= 10$,$AB = 5$,$PE = 2$时,线段PD的长为
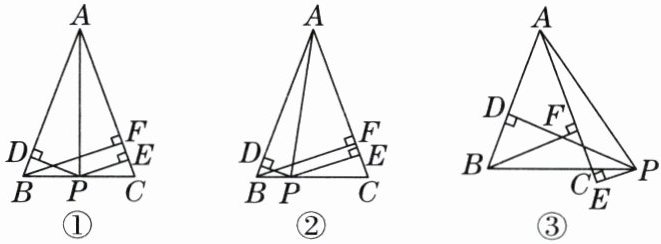
【问题情境】数学活动课上,老师提出了如下问题:如图,在△ABC中,$AB = AC$,P是BC上一点,过点P作$PD\perp AB$,$PE\perp AC$,垂足分别为D,E,过点B作$BF\perp AC$,垂足为F,连接AP.
【特例探究】(1)如图①,当P为BC边的中点时,利用面积之间的关系可以发现线段PD,PE,BF之间的数量关系为
BF=PD+PE
.【深入探究】(2)如图②,当P为BC边上的任意一点时,(1)中的数量关系是否仍然成立?若成立,请加以证明;若不成立,请写出成立的数量关系,并说明理由.
【拓展探究】(3)如图③,当点P在BC边的延长线上时:
①试猜想线段PD,PE,BF之间的数量关系,并证明你的猜想;
②当$S_{\triangle ABC}= 10$,$AB = 5$,$PE = 2$时,线段PD的长为
6
.
答案:
解:
(1)$BF=PD+PE$
(2)仍然成立.证明:$\because S_{\triangle ABC}=\frac{1}{2}AC× BF$,$S_{\triangle ABP}=\frac{1}{2}AB× PD$,$S_{\triangle ACP}=\frac{1}{2}AC× PE$,且$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,$\therefore \frac{1}{2}AC× BF=\frac{1}{2}AB× PD+\frac{1}{2}AC× PE$,$\because AB=AC$,$\therefore BF=PD+PE$.
(3)①$BF=PD-PE$.证明:$\because S_{\triangle ABC}=\frac{1}{2}AC× BF$,$S_{\triangle ABP}=\frac{1}{2}AB× PD$,$S_{\triangle ACP}=\frac{1}{2}AC× PE$,且$S_{\triangle ABC}=S_{\triangle ABP}-S_{\triangle ACP}$,$\therefore \frac{1}{2}AC× BF=\frac{1}{2}AB× PD-\frac{1}{2}AC× PE$,$\because AB=AC$,$\therefore BF=PD-PE$.②6
(1)$BF=PD+PE$
(2)仍然成立.证明:$\because S_{\triangle ABC}=\frac{1}{2}AC× BF$,$S_{\triangle ABP}=\frac{1}{2}AB× PD$,$S_{\triangle ACP}=\frac{1}{2}AC× PE$,且$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$,$\therefore \frac{1}{2}AC× BF=\frac{1}{2}AB× PD+\frac{1}{2}AC× PE$,$\because AB=AC$,$\therefore BF=PD+PE$.
(3)①$BF=PD-PE$.证明:$\because S_{\triangle ABC}=\frac{1}{2}AC× BF$,$S_{\triangle ABP}=\frac{1}{2}AB× PD$,$S_{\triangle ACP}=\frac{1}{2}AC× PE$,且$S_{\triangle ABC}=S_{\triangle ABP}-S_{\triangle ACP}$,$\therefore \frac{1}{2}AC× BF=\frac{1}{2}AB× PD-\frac{1}{2}AC× PE$,$\because AB=AC$,$\therefore BF=PD-PE$.②6
查看更多完整答案,请扫码查看


