《2025年点拨训练八年级数学上册沪科版安徽专版》

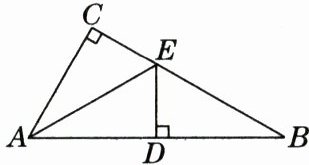
17. 如图,在 $ Rt \triangle ACB $ 中,$ \angle C = 90° $,$ \angle B = 30° $,点 $ E $ 在 $ BC $ 上,作 $ ED \perp AB $ 于点 $ D $,且 $ EC = ED $. 求证：$ D $ 为 $ AB $ 的中点.

答案： 证明:
∵ED⊥AB,
∴∠ADE=90°. 在Rt△ADE和Rt△ACE中，
∵$\left\{\begin{array}{l} AE=AE,\\ DE=CE,\end{array}\right. $
∴Rt△ADE≌Rt△ACE,
∴∠CAE=∠DAE. 在Rt△ACB中,∠CAE+∠DAE+∠B=90°,∠B=30°,
∴∠CAE=∠DAE=∠B=30°,
∴EA=EB.
∵ED⊥AB,
∴AD=BD,即D为AB的中点.

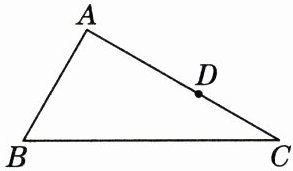
18. 如图,已知在 $ \triangle ABC $ 中,点 $ D $ 在边 $ AC $ 上,且 $ AB = AD $,$ \angle B = 2 \angle C $.
(1) 尺规作图：作 $ \angle BAC $ 的平分线 $ AP $,交 $ BC $ 于点 $ P $；(保留作图痕迹,不写作法)
(2) 在(1)的条件下,求证：点 $ D $ 在线段 $ PC $ 的垂直平分线上.

答案：

(1)解:如图，射线AP即为所作.
(2)证明:如图，连接PD.
∵AP平分∠BAC,
∴∠PAB=∠PAD. 又
∵AB=AD,AP=AP,
∴△PAB≌△PAD.
∴∠B=∠ADP.
∵∠B=2∠C,∠ADP=∠DPC+∠C,
∴2∠C=∠DPC+∠C,
∴∠DPC=∠C,
∴DP=DC,
∴点D在线段PC的垂直平分线上.

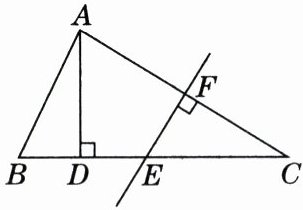
19. 如图,在 $ \triangle ABC $ 中,$ EF $ 是 $ AC $ 的垂直平分线,$ AD \perp BC $,$ D $ 为线段 $ BE $ 的中点.
(1) 求证：$ AB = CE $；
(2) 若 $ \angle C = 32° $,求 $ \angle BAC $ 的度数.

答案：
(1)证明:连接AE.
∵AD⊥BC,且D为线段BE 的中点，
∴AD垂直平分线段BE,
∴AB=AE.
∵EF垂直平分线段AC，
∴AE=CE,
∴AB=CE.
(2)解:∠BAC=84°.