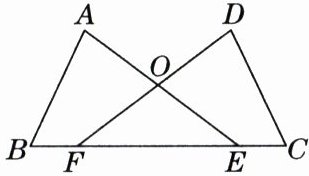
19. 如图,点E,F在线段BC上,BF= CE,AB= DC,AE= DF.
(1) 求证:△ABE≌△DCF;
(2) 若∠AEB= 40°,求∠AOF的度数.
(1) 求证:△ABE≌△DCF;
(2) 若∠AEB= 40°,求∠AOF的度数.

答案:
(1)证明:
∵BF=CE,
∴BE=CF.在△ABE和△DCF中,$\left\{\begin{array}{l} BE=CF,\\ AB=DC,\\ AE=DF,\end{array}\right. $
∴△ABE≌△DCF(SSS).
(2)解:
∵△ABE≌△DCF,
∴∠AEB=∠DFC=40°,
∴∠AOF=∠AEB+∠DFC=80°.
(1)证明:
∵BF=CE,
∴BE=CF.在△ABE和△DCF中,$\left\{\begin{array}{l} BE=CF,\\ AB=DC,\\ AE=DF,\end{array}\right. $
∴△ABE≌△DCF(SSS).
(2)解:
∵△ABE≌△DCF,
∴∠AEB=∠DFC=40°,
∴∠AOF=∠AEB+∠DFC=80°.
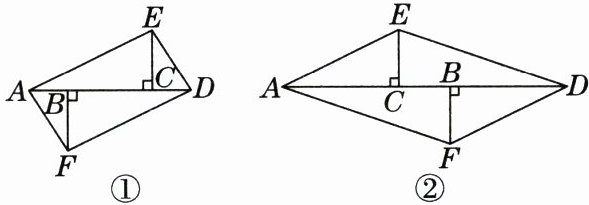
20. 如图①,点A,B,C,D在同一直线上,AB= CD,作EC⊥AD于点C,FB⊥AD于点B,且AE= DF,连接AF,ED.
(1) 求证:AF//DE且AF= DE.
(2) 若将△BFD沿AD方向平移得到图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
(1) 求证:AF//DE且AF= DE.
(2) 若将△BFD沿AD方向平移得到图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.

答案:
1. (1)
证明:
因为$EC\perp AD$,$FB\perp AD$,所以$\angle ACE = \angle DBF=90^{\circ}$。
又因为$AB = CD$,所以$AB + BC=CD + BC$,即$AC = DB$。
在$Rt\triangle ACE$和$Rt\triangle DBF$中,$\left\{\begin{array}{l}AE = DF\\AC = DB\end{array}\right.$。
根据$HL$(斜边 - 直角边)定理,$Rt\triangle ACE\cong Rt\triangle DBF$。
所以$\angle EAC=\angle FDB$。
在$\triangle ABF$和$\triangle DCE$中,$\left\{\begin{array}{l}AB = CD\\\angle ABF=\angle DCE = 90^{\circ}\\\angle BAF=\angle CDE\end{array}\right.$。
根据$ASA$(角 - 边 - 角)定理,$\triangle ABF\cong\triangle DCE$。
所以$AF = DE$,$\angle AFB=\angle DEC$。
因为$\angle AFB+\angle FAB = 90^{\circ}$,$\angle DEC+\angle EDC = 90^{\circ}$,且$\angle FAB=\angle EDC$,所以$\angle AFD=\angle DEA$。
所以$AF// DE$。
2. (2)
结论仍成立。
理由:
因为$EC\perp AD$,$FB\perp AD$,所以$\angle ACE=\angle DBF = 90^{\circ}$。
又因为$AB = CD$,所以$AC = DB$。
在$Rt\triangle ACE$和$Rt\triangle DBF$中,$\left\{\begin{array}{l}AE = DF\\AC = DB\end{array}\right.$。
根据$HL$定理,$Rt\triangle ACE\cong Rt\triangle DBF$,所以$\angle EAC=\angle FDB$。
因为$AB = CD$,$\angle ABF=\angle DCE = 90^{\circ}$。
在$\triangle ABF$和$\triangle DCE$中,$\left\{\begin{array}{l}AB = CD\\\angle BAF=\angle CDE\\\angle ABF=\angle DCE\end{array}\right.$。
根据$ASA$定理,$\triangle ABF\cong\triangle DCE$。
所以$AF = DE$,$\angle AFB=\angle DEC$。
因为$\angle AFB+\angle FAB = 90^{\circ}$,$\angle DEC+\angle EDC = 90^{\circ}$,且$\angle FAB=\angle EDC$,所以$\angle AFD=\angle DEA$。
所以$AF// DE$。
综上,(1)得证$AF// DE$且$AF = DE$;(2)(1)中的结论仍成立。
证明:
因为$EC\perp AD$,$FB\perp AD$,所以$\angle ACE = \angle DBF=90^{\circ}$。
又因为$AB = CD$,所以$AB + BC=CD + BC$,即$AC = DB$。
在$Rt\triangle ACE$和$Rt\triangle DBF$中,$\left\{\begin{array}{l}AE = DF\\AC = DB\end{array}\right.$。
根据$HL$(斜边 - 直角边)定理,$Rt\triangle ACE\cong Rt\triangle DBF$。
所以$\angle EAC=\angle FDB$。
在$\triangle ABF$和$\triangle DCE$中,$\left\{\begin{array}{l}AB = CD\\\angle ABF=\angle DCE = 90^{\circ}\\\angle BAF=\angle CDE\end{array}\right.$。
根据$ASA$(角 - 边 - 角)定理,$\triangle ABF\cong\triangle DCE$。
所以$AF = DE$,$\angle AFB=\angle DEC$。
因为$\angle AFB+\angle FAB = 90^{\circ}$,$\angle DEC+\angle EDC = 90^{\circ}$,且$\angle FAB=\angle EDC$,所以$\angle AFD=\angle DEA$。
所以$AF// DE$。
2. (2)
结论仍成立。
理由:
因为$EC\perp AD$,$FB\perp AD$,所以$\angle ACE=\angle DBF = 90^{\circ}$。
又因为$AB = CD$,所以$AC = DB$。
在$Rt\triangle ACE$和$Rt\triangle DBF$中,$\left\{\begin{array}{l}AE = DF\\AC = DB\end{array}\right.$。
根据$HL$定理,$Rt\triangle ACE\cong Rt\triangle DBF$,所以$\angle EAC=\angle FDB$。
因为$AB = CD$,$\angle ABF=\angle DCE = 90^{\circ}$。
在$\triangle ABF$和$\triangle DCE$中,$\left\{\begin{array}{l}AB = CD\\\angle BAF=\angle CDE\\\angle ABF=\angle DCE\end{array}\right.$。
根据$ASA$定理,$\triangle ABF\cong\triangle DCE$。
所以$AF = DE$,$\angle AFB=\angle DEC$。
因为$\angle AFB+\angle FAB = 90^{\circ}$,$\angle DEC+\angle EDC = 90^{\circ}$,且$\angle FAB=\angle EDC$,所以$\angle AFD=\angle DEA$。
所以$AF// DE$。
综上,(1)得证$AF// DE$且$AF = DE$;(2)(1)中的结论仍成立。
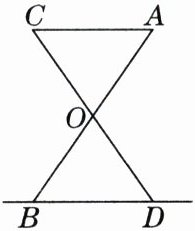
21. 小红家的阳台上放置了一个落地式晒衣架. 如图是该晒衣架的侧面示意图,B,D两点置于地面上,AC//BD,现将晒衣架完全展开并稳固,经测量有OA= OB. AB,CD的交点O距离地面的高度为48 cm. 若小红的连衣裙挂在衣架AC上,总长度为100 cm,此时连衣裙是否会碰到地面?请通过计算说明理由.

答案:
解:连衣裙会碰到地面。
过点$O$作$OE \perp BD$于点$E$,则$OE = 48\ cm$。
因为$AC // BD$,所以$\angle OAC=\angle OBD$,$\angle OCA=\angle ODB$。
所以$\triangle AOC \backsim \triangle BOD$。
因为$OA = OB$,设$OA = OB = x$,$OC = y$,则$OD=\frac{OB}{OA}\cdot OC = y$(相似比为$1$),即$OC = OD$。
过点$C$作$CF \perp BD$于点$F$,则$OE // CF$。
在$\triangle CDF$中,$\frac{OE}{CF}=\frac{OD}{CD}=\frac{OD}{OC + OD}=\frac{1}{2}$。
所以$CF = 2OE=2×48 = 96\ cm$。
因为$96\ cm<100\ cm$,所以连衣裙会碰到地面。
过点$O$作$OE \perp BD$于点$E$,则$OE = 48\ cm$。
因为$AC // BD$,所以$\angle OAC=\angle OBD$,$\angle OCA=\angle ODB$。
所以$\triangle AOC \backsim \triangle BOD$。
因为$OA = OB$,设$OA = OB = x$,$OC = y$,则$OD=\frac{OB}{OA}\cdot OC = y$(相似比为$1$),即$OC = OD$。
过点$C$作$CF \perp BD$于点$F$,则$OE // CF$。
在$\triangle CDF$中,$\frac{OE}{CF}=\frac{OD}{CD}=\frac{OD}{OC + OD}=\frac{1}{2}$。
所以$CF = 2OE=2×48 = 96\ cm$。
因为$96\ cm<100\ cm$,所以连衣裙会碰到地面。
查看更多完整答案,请扫码查看


