23. 【问题提出】同学们,我们知道利用“SSA”不能判定两个三角形全等. 我们准备对“满足两边和其中一边的对角对应相等的两个三角形是否全等”进行研究.
【初步思考】不妨将问题用符号语言表示为:在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,然后对∠B进行分类,可分为∠B是直角、钝角、锐角三种情况进行探究.
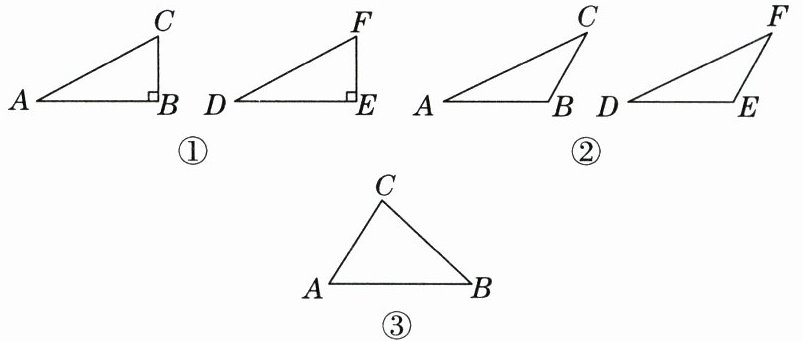
【深入探究】(1) 当∠B是直角时,△ABC≌△DEF. 如图①,在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E= 90°,根据判定方法______,可以证得Rt△ABC≌Rt△DEF.
(2) 当∠B是钝角时,△ABC≌△DEF. 如图②,在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,且∠B,∠E都是钝角,请说明△ABC≌△DEF.
(3) 当∠B是锐角时,△ABC和△DEF不一定全等. 在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,且∠B,∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写作法,但保留作图痕迹).
【初步思考】不妨将问题用符号语言表示为:在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,然后对∠B进行分类,可分为∠B是直角、钝角、锐角三种情况进行探究.
【深入探究】(1) 当∠B是直角时,△ABC≌△DEF. 如图①,在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E= 90°,根据判定方法______,可以证得Rt△ABC≌Rt△DEF.
(2) 当∠B是钝角时,△ABC≌△DEF. 如图②,在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,且∠B,∠E都是钝角,请说明△ABC≌△DEF.
(3) 当∠B是锐角时,△ABC和△DEF不一定全等. 在△ABC和△DEF中,AC= DF,BC= EF,∠B= ∠E,且∠B,∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写作法,但保留作图痕迹).

答案:
解:
(1)HL
(2)过点C作CG⊥AB,交AB的延长线于点G,过点F 作FH⊥DE,交DE的延长线于点H,则∠AGC=∠DHF=90°.
∵∠ABC=∠DEF,
∴∠CBG=∠FEH.又
∵BC=EF,
∴△CBG≌△FEH.
∴CG=FH.在Rt△ACG和Rt△DFH中,
∵$\left\{\begin{array}{l} AC=DF,\\ CG=FH,\end{array}\right. $
∴Rt△ACG≌Rt△DFH.
∴∠A=∠D.又
∵∠ABC=∠DEF,BC=EF,
∴△ABC≌△DEF.
(3)如图.
解:
(1)HL
(2)过点C作CG⊥AB,交AB的延长线于点G,过点F 作FH⊥DE,交DE的延长线于点H,则∠AGC=∠DHF=90°.
∵∠ABC=∠DEF,
∴∠CBG=∠FEH.又
∵BC=EF,
∴△CBG≌△FEH.
∴CG=FH.在Rt△ACG和Rt△DFH中,
∵$\left\{\begin{array}{l} AC=DF,\\ CG=FH,\end{array}\right. $
∴Rt△ACG≌Rt△DFH.
∴∠A=∠D.又
∵∠ABC=∠DEF,BC=EF,
∴△ABC≌△DEF.
(3)如图.

查看更多完整答案,请扫码查看


