21. 如图,有三摞相同规格的碗整齐地叠放在桌面上,图中标注了相关数据,请根据这些信息解答下列问题。
(1) 最底层的碗的高度是
(2) 求第三摞碗的总高度 $ y(cm) $ 与碗的总个数 $ x $(个)之间的函数关系式,并通过计算判断这摞碗的高度能否是 $ 1m $;
(3) 已知买一个碗需要 2 元,对于第三摞碗,若其高度不低于 $ 1.5m $,求买这摞碗至少需要多少钱。
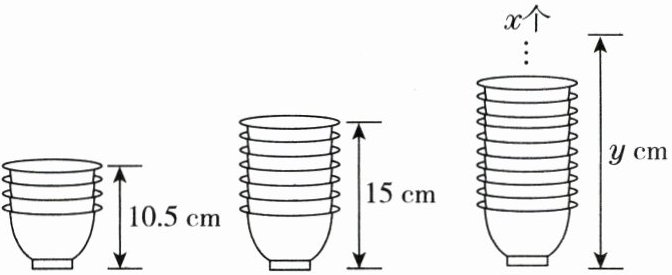
(1) 最底层的碗的高度是
6
$ cm $,每增加一个碗,高度增加______ 1.5
$ cm $;(2) 求第三摞碗的总高度 $ y(cm) $ 与碗的总个数 $ x $(个)之间的函数关系式,并通过计算判断这摞碗的高度能否是 $ 1m $;
(3) 已知买一个碗需要 2 元,对于第三摞碗,若其高度不低于 $ 1.5m $,求买这摞碗至少需要多少钱。

答案:
解:
(1)6;1.5
(2)y=6+(x-1)×1.5=1.5x+4.5,1m=100cm,当y=100时,1.5x+4.5=100,解得x=191/3,因为191/3不是整数,所以这摞碗的高度不能是1m.
(3)1.5m=150cm,对于y=1.5x+4.5,当y≥150,即1.5x+4.5≥150时,x≥97,所以买这摞碗至少需要97×2=194(元).
(1)6;1.5
(2)y=6+(x-1)×1.5=1.5x+4.5,1m=100cm,当y=100时,1.5x+4.5=100,解得x=191/3,因为191/3不是整数,所以这摞碗的高度不能是1m.
(3)1.5m=150cm,对于y=1.5x+4.5,当y≥150,即1.5x+4.5≥150时,x≥97,所以买这摞碗至少需要97×2=194(元).
22. 在 $ \triangle ABC $ 中,$ \angle ABC = \angle ACB $,$ D $ 为线段 $ CB $ 上一点(不与点 $ C $,$ B $ 重合),$ E $ 为射线 $ CA $ 上一点,$ \angle ADE = \angle AED $。设 $ \angle BAD = \alpha $,$ \angle CDE = \beta $。
(1) 如图①,点 $ E $ 在线段 $ AC $ 上。①若 $ \angle BAC = 42^{\circ} $,$ \angle DAE = 30^{\circ} $,则 $ \alpha = $
② $ \alpha $ 与 $ \beta $ 的数量关系为
(2) 如图②,当点 $ E $ 在 $ CA $ 的延长线上时,写出 $ \alpha $ 与 $ \beta $ 的数量关系,并说明理由
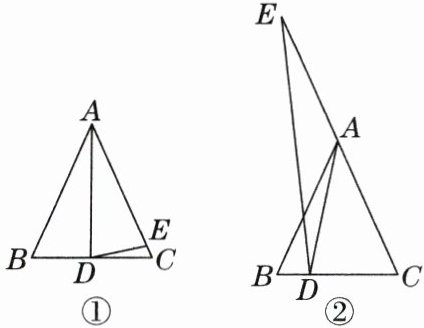
2β=180°+α,理由如下:
设∠BAC=x,∠DAE=y
α=x-(180°-y)=x-180°+y
∵∠ACB=∠ABC
∴∠ACB=180°-x2
∵∠ADE=∠AED
∴∠AED=180°-y2
∵∠EDB是△EDC的一个外角
∴∠EDB=∠AED+∠ACB
∴180°-β=180°-y2+180°-x2
∴2β=x+y
∴2β=180°+α
(1) 如图①,点 $ E $ 在线段 $ AC $ 上。①若 $ \angle BAC = 42^{\circ} $,$ \angle DAE = 30^{\circ} $,则 $ \alpha = $
12°
,$ \beta = $6°
;② $ \alpha $ 与 $ \beta $ 的数量关系为
α=2β
;(2) 如图②,当点 $ E $ 在 $ CA $ 的延长线上时,写出 $ \alpha $ 与 $ \beta $ 的数量关系,并说明理由

2β=180°+α,理由如下:
设∠BAC=x,∠DAE=y
α=x-(180°-y)=x-180°+y
∵∠ACB=∠ABC
∴∠ACB=180°-x2
∵∠ADE=∠AED
∴∠AED=180°-y2
∵∠EDB是△EDC的一个外角
∴∠EDB=∠AED+∠ACB
∴180°-β=180°-y2+180°-x2
∴2β=x+y
∴2β=180°+α
答案:
$(1)①12°;6° ②α=2β$
∵$∠ACB=∠ABC$
∴$∠ACB=\frac{180°-x}{2}$
∵$∠ADE=∠AED$
∴$∠AED=\frac{180°-y}{2}$
∴$∠EDB$是$△EDC$是一个外角
∴$∠EDB=∠AED+∠ACB$
∴$180°-β=\frac{180°-y}{2}+\frac{180°-x}{2}$
∴$2β=x+y$
∴$2β=180°+α$
$(2)2β=180°+α,$理由如下$.$
设$∠BAC=x,∠DAE=y$
$a=x-(180°-y)=x-180°+y$
∵$∠ACB=∠ABC$
∴$∠ACB=\frac{180°-x}{2}$
∵$∠ADE=∠AED$
∴$∠AED=\frac{180°-y}{2}$
∴$∠EDB$是$△EDC$是一个外角
∴$∠EDB=∠AED+∠ACB$
∴$180°-β=\frac{180°-y}{2}+\frac{180°-x}{2}$
∴$2β=x+y$
∴$2β=180°+α$
查看更多完整答案,请扫码查看


