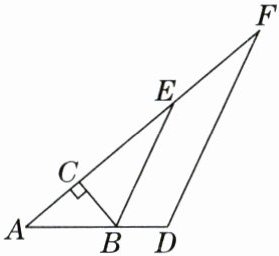
19. (10分)如图,在△ABC中,$\angle ACB = 90^{\circ}$,$\angle A = 40^{\circ}$,△ABC的外角$\angle CBD$的平分线BE交AC的延长线于点E.
(1)求$\angle CBE$的度数;
(2)过点D作$DF// BE$,交AC的延长线于点F,求$\angle F$的度数.
(1)求$\angle CBE$的度数;
(2)过点D作$DF// BE$,交AC的延长线于点F,求$\angle F$的度数.

答案:
解:
(1)$\angle CBE=65°$.
(2)$\angle F=25°$.
(1)$\angle CBE=65°$.
(2)$\angle F=25°$.
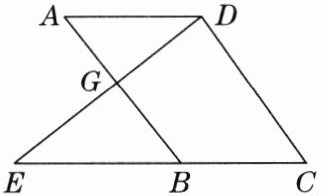
20. 如图,E,B,C三点共线,AB与DE交于点G. 已知$\angle A= \angle C$,若$AB// CD$,则$BC// AD$. 请补全证明过程,并解答下列问题.
(1)证明:$\because AB// CD$(已知),
$\therefore\angle ABE= \angle C$(
$\because\angle A= \angle C$(已知),
$\therefore\angle ABE= $
$\therefore BC// AD$(
(2)【延伸】若前提“$\angle A= \angle C$”不变,将条件“$AB// CD$”与结论“$BC// AD$”调换,所得命题是真命题还是假命题?如果是真命题,写出证明过程;如果是假命题,举出反例.
(3)【拓展】如图,已知有三个论断①$\angle A= \angle C$;②$AB// CD$;③$BC// AD$,选出其中两个作为条件,另一个作为结论组成一个命题,能组成多少个真命题?
(1)证明:$\because AB// CD$(已知),
$\therefore\angle ABE= \angle C$(
两直线平行,同位角相等
).$\because\angle A= \angle C$(已知),
$\therefore\angle ABE= $
$\angle A$
(等量代换),$\therefore BC// AD$(
内错角相等,两直线平行
).(2)【延伸】若前提“$\angle A= \angle C$”不变,将条件“$AB// CD$”与结论“$BC// AD$”调换,所得命题是真命题还是假命题?如果是真命题,写出证明过程;如果是假命题,举出反例.
(3)【拓展】如图,已知有三个论断①$\angle A= \angle C$;②$AB// CD$;③$BC// AD$,选出其中两个作为条件,另一个作为结论组成一个命题,能组成多少个真命题?

答案:
解:
(1)两直线平行,同位角相等;$\angle A$;内错角相等,两直线平行
(2)是真命题.证明:$\because BC// AD$,$\therefore \angle ABE=\angle A$,$\because \angle A=\angle C$,$\therefore \angle ABE=\angle C$,$\therefore AB// CD$,故将条件“$AB// CD$”与结论“$BC// AD$”调换后所得命题为真命题.
(3)根据题意可知,①②作为条件,③作为结论,为真命题;①③作为条件,②作为结论,为真命题;②③作为条件,①作为结论,为真命题.故能组成3个真命题.
(1)两直线平行,同位角相等;$\angle A$;内错角相等,两直线平行
(2)是真命题.证明:$\because BC// AD$,$\therefore \angle ABE=\angle A$,$\because \angle A=\angle C$,$\therefore \angle ABE=\angle C$,$\therefore AB// CD$,故将条件“$AB// CD$”与结论“$BC// AD$”调换后所得命题为真命题.
(3)根据题意可知,①②作为条件,③作为结论,为真命题;①③作为条件,②作为结论,为真命题;②③作为条件,①作为结论,为真命题.故能组成3个真命题.
查看更多完整答案,请扫码查看


