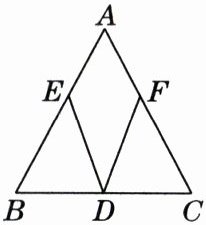
15. 如图,已知点D为BC的中点,∠EDC= ∠FDB,∠B= ∠C. 求证:△BDE≌△CDF.

答案:
证明:
∵点D为BC的中点,
∴BD=CD。
在△BDE和△CDF中,
∠B=∠C(已知),
BD=CD(已证),
∠FDB=∠EDC(已知),
∴△BDE≌△CDF(ASA)。
∵点D为BC的中点,
∴BD=CD。
在△BDE和△CDF中,
∠B=∠C(已知),
BD=CD(已证),
∠FDB=∠EDC(已知),
∴△BDE≌△CDF(ASA)。
16. 阅读下面材料,完成相应填空.
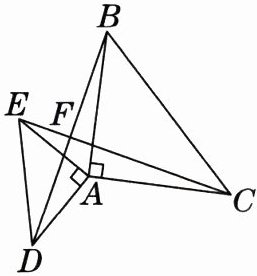
如图,已知AB⊥AC,AD⊥AE,AB= AC,AD= AE.
求证:DB⊥EC.
证明:如图,设BD和CE交于点F.
∵AB⊥AC,AD⊥AE,∴
∴∠BAC+
∠ABC+∠ACB= 90°. ∴∠CAE= ∠BAD.
在△ADB和△AEC中,
∵$\begin{cases}AB= AC, \\ ∠BAD= ∠CAE, \\ AD= AE,\end{cases} $
∴△ADB≌△AEC(
∴∠CBD+∠BCE= ∠ABC+∠ABD+∠BCE= ∠ABC+
∴DB⊥EC.
如图,已知AB⊥AC,AD⊥AE,AB= AC,AD= AE.
求证:DB⊥EC.
证明:如图,设BD和CE交于点F.
∵AB⊥AC,AD⊥AE,∴
∠BAC
= ∠DAE
= 90°,∴∠BAC+
∠BAE
= ∠DAE+∠BAE
,∠ABC+∠ACB= 90°. ∴∠CAE= ∠BAD.
在△ADB和△AEC中,
∵$\begin{cases}AB= AC, \\ ∠BAD= ∠CAE, \\ AD= AE,\end{cases} $
∴△ADB≌△AEC(
SAS
),∴∠ACE= ∠ABD.∴∠CBD+∠BCE= ∠ABC+∠ABD+∠BCE= ∠ABC+
∠ACE
+∠BCE= ∠ABC+∠ACB
= 90°,∴∠BFC
= 90°,∴DB⊥EC.

答案:
∠BAC;∠DAE;∠BAE;∠BAE;SAS;∠ACE;∠ACB;∠BFC
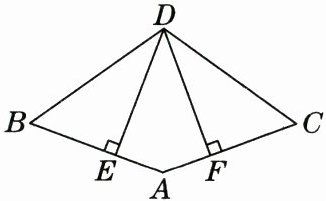
17. 如图,AB= AC,BD= CD,DE⊥AB,垂足为E,DF⊥AC,垂足为F. 求证:DE= DF.

答案:
证明:连接AD。
在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS)。
∴∠BAD=∠CAD。
∵DE⊥AB,DF⊥AC,
∴DE=DF(角平分线上的点到角两边的距离相等)。
在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS)。
∴∠BAD=∠CAD。
∵DE⊥AB,DF⊥AC,
∴DE=DF(角平分线上的点到角两边的距离相等)。
18. 如图,在△ABC中,AB= AC,AB>BC,点D在边BC上,点E,F在线段AD上,且DF= 2AF,∠1= ∠2= ∠BAC.
(1) 求证:∠ABE= ∠CAF;
(2) 若AD= 12,则BE的长为_________
(1) 求证:∠ABE= ∠CAF;
(2) 若AD= 12,则BE的长为_________
4
$.zyjl.cn/pic18/2025-07-18/76b7003bd98edba984bb1268d0d37f41.jpg?x-oss-process=image/crop,x_2430,y_0,w_1260,h_2690/crop,x_868,y_2126,w_239,h_281">$
答案:
(1)证明:
∵∠1=∠BAE+∠ABE,∠1=∠BAC,
∴∠BAC=∠BAE+∠ABE,又
∵∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF.
(2) 4
(1)证明:
∵∠1=∠BAE+∠ABE,∠1=∠BAC,
∴∠BAC=∠BAE+∠ABE,又
∵∠BAC=∠BAE+∠CAF,
∴∠ABE=∠CAF.
(2) 4
查看更多完整答案,请扫码查看


