《2025年点拨训练八年级数学上册沪科版安徽专版》

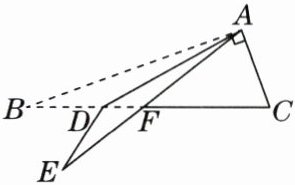
21. 如图,在△ABC中,$\angle BAC = 90^{\circ}$,点D是边BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F. 若$\angle C-\angle B = 50^{\circ}$,$\angle BAD = x^{\circ}(0 ＜ x\leqslant45)$.
(1)求$\angle B$的度数；
(2)若△DEF中有两个角相等,求x的值.

答案： 解：
(1)$\angle B=20°$.
(2)$x=30$.

22. 定义：在一个三角形中,若其中一个角是另一个角的2倍,我们称这两个角互为“开心角”,这个三角形叫作“开心三角形”. 例如,在△ABC中,$\angle A = 70^{\circ}$,$\angle B = 35^{\circ}$,则$\angle A与\angle B$互为“开心角”,△ABC为“开心三角形”.
(1)若△ABC为开心三角形,$\angle A = 144^{\circ}$,则这个三角形中最小的内角为12°.
(2)若△ABC为开心三角形,$\angle A = 70^{\circ}$,则这个三角形中最小的内角为35°或$\left(\frac{110}{3}\right)°$.
(3)已知$\angle A$是开心三角形ABC中最小的内角,并且是其中的一个开心角,试确定$\angle A$的取值范围.
解：$\because \angle A$是开心三角形$ABC$中最小的内角，并且是其中的一个开心角，$\therefore$另一个开心角是$2\angle A$，$\therefore$第三个内角是$180° - 3\angle A$.$\because \angle A$是最小的内角，$\therefore \angle A\leqslant 180° - 3\angle A$，$\therefore \angle A\leqslant 45°$，$\therefore 0° ＜ \angle A\leqslant 45°$.

答案： 解：
(1)$12°$
(2)$35°$或$\left(\frac{110}{3}\right)°$
(3)$\because \angle A$是开心三角形$ABC$中最小的内角，并且是其中的一个开心角，$\therefore$另一个开心角是$2\angle A$，$\therefore$第三个内角是$180° - 3\angle A$.$\because \angle A$是最小的内角，$\therefore \angle A\leqslant 180° - 3\angle A$，$\therefore \angle A\leqslant 45°$，$\therefore 0° ＜ \angle A\leqslant 45°$.