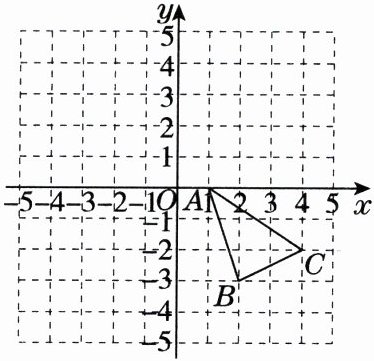
15. 如图,在平面直角坐标系中,已知$ \triangle ABC 的三个顶点的坐标分别为 A(1,0) $,$ B(2,-3) $,$ C(4,-2) $.
(1)画出$ \triangle ABC 关于 x 轴的对称图形 \triangle A_1B_1C_1 $;
(2)画出$ \triangle A_1B_1C_1 $向左平移5个单位长度后得到的$ \triangle A_2B_2C_2 $;
(3)如果$ AC 上有一点 P(m,n) $经过上述两次变换,那么对应$ A_2C_2 上的点 P_2 $的坐标是什么?
(1)画出$ \triangle ABC 关于 x 轴的对称图形 \triangle A_1B_1C_1 $;
(2)画出$ \triangle A_1B_1C_1 $向左平移5个单位长度后得到的$ \triangle A_2B_2C_2 $;
(3)如果$ AC 上有一点 P(m,n) $经过上述两次变换,那么对应$ A_2C_2 上的点 P_2 $的坐标是什么?

答案:
解:
(1)如图
(2)如图
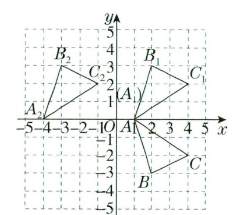
(3)(m-5,-n).
解:
(1)如图
(2)如图

(3)(m-5,-n).
16. 已知一次函数$ y = kx + b 的图象经过点 (-2,10) $,(3,0)和$ (1,m) $.
(1)求$ m $的值;
(2)当$ -4 \leq y \leq 8 $时,求$ x $的取值范围.
(1)求$ m $的值;
(2)当$ -4 \leq y \leq 8 $时,求$ x $的取值范围.
答案:
解:
(1)m=4.
(2)x的取值范围为-1≤x≤5.
(1)m=4.
(2)x的取值范围为-1≤x≤5.
17. 从①$ \angle 1 + \angle 2 = 180^{\circ} $;②$ \angle 3 = \angle A $;③$ \angle B = \angle C $三个条件中选出两个作为题设,另一个作为结论可以组成三个命题.从中选择一个真命题,写出已知、求证,并证明.
如图,已知:
证明:
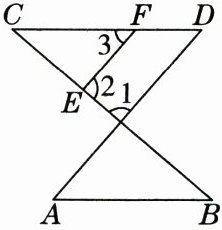
如图,已知:
①②
,求证:______③
.(填序号)证明:

答案:
解:(答案不唯一)①②;③
∵∠1+∠2=180°,
∴AD//EF,
∴∠3=∠D.
∵∠3=∠A,
∴∠A=∠D,
∴AB//CD,
∴∠B=∠C.
∵∠1+∠2=180°,
∴AD//EF,
∴∠3=∠D.
∵∠3=∠A,
∴∠A=∠D,
∴AB//CD,
∴∠B=∠C.
查看更多完整答案,请扫码查看


