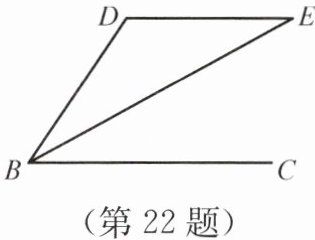
22. 如图所示,已知 $ DE // BC $,$ \angle D : \angle DBC = 2 : 1 $,$ \angle CBE = \angle DBE $,
(1)求 $ \angle DEB $ 的度数;
(2)过点 $ E $ 作 $ EF \perp BD $,垂足为 $ F $.求证:$ ED $ 平分 $ \angle BEF $.
(1)求 $ \angle DEB $ 的度数;
(2)过点 $ E $ 作 $ EF \perp BD $,垂足为 $ F $.求证:$ ED $ 平分 $ \angle BEF $.

答案:
1. (1)
因为$DE// BC$,根据两直线平行,同旁内角互补,所以$\angle D+\angle DBC = 180^{\circ}$。
又因为$\angle D:\angle DBC = 2:1$,设$\angle DBC=x$,则$\angle D = 2x$。
那么$2x + x=180^{\circ}$,即$3x = 180^{\circ}$,解得$x = 60^{\circ}$,所以$\angle DBC = 60^{\circ}$。
因为$\angle CBE=\angle DBE$,且$\angle DBC=\angle DBE+\angle CBE$,所以$\angle DBE=\frac{1}{2}\angle DBC$。
把$\angle DBC = 60^{\circ}$代入,得$\angle DBE = 30^{\circ}$。
再由$DE// BC$,根据两直线平行,内错角相等,所以$\angle DEB=\angle EBC$。
而$\angle EBC=\angle DBE$,所以$\angle DEB = 30^{\circ}$。
2. (2)
证明:因为$EF\perp BD$,所以$\angle EFD = 90^{\circ}$。
由$DE// BC$,可得$\angle D=\angle DBC = 120^{\circ}$(前面已求得$\angle DBC = 60^{\circ}$,$\angle D = 120^{\circ}$)。
在$\triangle DEF$中,$\angle DEF=180^{\circ}-\angle D-\angle EFD$。
把$\angle D = 120^{\circ}$,$\angle EFD = 90^{\circ}$代入,得$\angle DEF=180^{\circ}-120^{\circ}-90^{\circ}+ \angle DEB$(这里利用$\angle D+\angle DEB+\angle BEF+\angle EFD = 360^{\circ}$,$\angle BEF=\angle BED+\angle DEF$)。
因为$\angle DEB = 30^{\circ}$,$\angle DEF = 60^{\circ}$($\angle D = 120^{\circ}$,$\angle EFD = 90^{\circ}$,$\angle DEF=180^{\circ}-\angle D-\angle EFD$,$\angle DEF = 180 - 120-90+\angle DEB$,$\angle DEF = 60^{\circ}$)。
又因为$\angle DEB = 30^{\circ}$,所以$\angle DEF=\angle DEB$。
综上,(1)$\angle DEB = 30^{\circ}$;(2)证明过程如上述。
因为$DE// BC$,根据两直线平行,同旁内角互补,所以$\angle D+\angle DBC = 180^{\circ}$。
又因为$\angle D:\angle DBC = 2:1$,设$\angle DBC=x$,则$\angle D = 2x$。
那么$2x + x=180^{\circ}$,即$3x = 180^{\circ}$,解得$x = 60^{\circ}$,所以$\angle DBC = 60^{\circ}$。
因为$\angle CBE=\angle DBE$,且$\angle DBC=\angle DBE+\angle CBE$,所以$\angle DBE=\frac{1}{2}\angle DBC$。
把$\angle DBC = 60^{\circ}$代入,得$\angle DBE = 30^{\circ}$。
再由$DE// BC$,根据两直线平行,内错角相等,所以$\angle DEB=\angle EBC$。
而$\angle EBC=\angle DBE$,所以$\angle DEB = 30^{\circ}$。
2. (2)
证明:因为$EF\perp BD$,所以$\angle EFD = 90^{\circ}$。
由$DE// BC$,可得$\angle D=\angle DBC = 120^{\circ}$(前面已求得$\angle DBC = 60^{\circ}$,$\angle D = 120^{\circ}$)。
在$\triangle DEF$中,$\angle DEF=180^{\circ}-\angle D-\angle EFD$。
把$\angle D = 120^{\circ}$,$\angle EFD = 90^{\circ}$代入,得$\angle DEF=180^{\circ}-120^{\circ}-90^{\circ}+ \angle DEB$(这里利用$\angle D+\angle DEB+\angle BEF+\angle EFD = 360^{\circ}$,$\angle BEF=\angle BED+\angle DEF$)。
因为$\angle DEB = 30^{\circ}$,$\angle DEF = 60^{\circ}$($\angle D = 120^{\circ}$,$\angle EFD = 90^{\circ}$,$\angle DEF=180^{\circ}-\angle D-\angle EFD$,$\angle DEF = 180 - 120-90+\angle DEB$,$\angle DEF = 60^{\circ}$)。
又因为$\angle DEB = 30^{\circ}$,所以$\angle DEF=\angle DEB$。
综上,(1)$\angle DEB = 30^{\circ}$;(2)证明过程如上述。
23. 风力发电因其既可再生又不破坏生态环境的特点,深受各国欢迎,并被大规模推广和实施.据统计,我国 $ 2024 $ 年上半年全国风力发电量为 $ 5.1 × 10^{11} $ 度,若某市有 $ 40 $ 万户居民,平均每户年用电量是 $ 2.55 × 10^3 $ 度,那么我国 $ 2024 $ 年上半年由风力所发的电量可供该市居民使用多少年?
答案:
500.
查看更多完整答案,请扫码查看


