23. 如图所示,有三个论断:① $ \angle 1 = \angle 2 $;② $ \angle B = \angle D $;③ $ \angle A = \angle C $,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.


答案:
答案不唯一,如:已知 $\angle 1=\angle 2$,$\angle B=\angle D$,求证 $\angle A=\angle C$. 证明:$\because \angle 1=\angle D M C$,$\angle 1=\angle 2$,$\therefore \angle 2=\angle D M C$. $\therefore D E // B F$. $\therefore \angle B=\angle A E D$.$\because \angle B=\angle D$,$\therefore \angle D=\angle A E D$. $\therefore A B // D C$. $\therefore \angle A=\angle C$.
24. 生活中经常会遇到一些不可直接测量的距离或角度,为了测量出这些距离和角度,项目学习小组进行了如下探究:

(1)项目A中,利用图形对称性质:
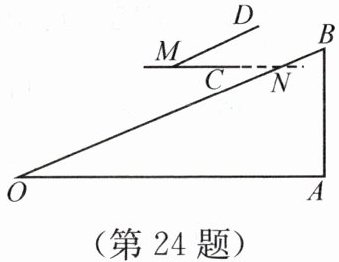
(2)项目B中,利用了物理中的重力原理与数学中的平行线的性质. 如图是简化的测量方案示意图,其中,$ MC // OA $,$ MD // OB $,请你证明:$ \angle CMD = \angle O $.

(1)项目A中,利用图形对称性质:
成中心对称的两个图形重合,对应边相等
.就可以得到$ AB = CD = 9 \text{ cm} $.(2)项目B中,利用了物理中的重力原理与数学中的平行线的性质. 如图是简化的测量方案示意图,其中,$ MC // OA $,$ MD // OB $,请你证明:$ \angle CMD = \angle O $.

证明:$\because M C // O A$,$\therefore \angle O=\angle O N M$. 又 $\because M D // O B$,$\therefore \angle C M D=\angle O N M$,$\therefore \angle C M D=\angle O$.
答案:
(1) 成中心对称的两个图形重合,对应边相等;
(2) 证明:$\because M C // O A$,$\therefore \angle O=\angle O N M$. 又 $\because M D // O B$,$\therefore \angle C M D=\angle O N M$,$\therefore \angle C M D=\angle O$.
(1) 成中心对称的两个图形重合,对应边相等;
(2) 证明:$\because M C // O A$,$\therefore \angle O=\angle O N M$. 又 $\because M D // O B$,$\therefore \angle C M D=\angle O N M$,$\therefore \angle C M D=\angle O$.
查看更多完整答案,请扫码查看


