20. 解不等式(组):
(1)$\frac{x-3}{4}<6-\frac{3-4x}{2}$,并把解集在数轴上表示出来;
(2)$\begin{cases}-3(x-2)>4-x\frac{1+2x}{3}>1-2x\end{cases} $
(1)$\frac{x-3}{4}<6-\frac{3-4x}{2}$,并把解集在数轴上表示出来;
(2)$\begin{cases}-3(x-2)>4-x\frac{1+2x}{3}>1-2x\end{cases} $
答案:
(1)$x>-3$,数轴略;
(2)$\frac {1}{4}<x<1$。
(1)$x>-3$,数轴略;
(2)$\frac {1}{4}<x<1$。
21. (1)完成下面的证明过程.
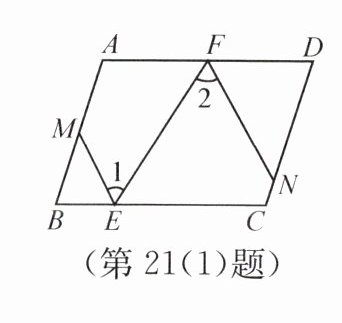
已知:如图,在四边形 ABCD 中,ABCD,$∠B= ∠D$,点 E,F 分别在边 BC,AD 上,EM 平分$∠BEF$交 AB 于点 M,FN 平分$∠DFE$交 CD 于点 N.
求证:$EM// FN$.
证明:在四边形 ABCD 中,
∵$AB// CD$,(已知)
∴____,(两直线平行,同旁内角互补)
∵$∠B= ∠D$,(已知)
∴$∠C+∠D= 180^{\circ}$,(____)
∴____,(同旁内角互补,两直线平行)
∴____.(两直线平行,内错角相等)
∵EM 平分$∠BEF$,FN 平分$∠DFE$,(已知)
∴$∠1= \frac{1}{2}∠BEF$,$∠2= \frac{1}{2}∠DFE$,(____)
∴$∠1= ∠2$,(等量代换)
∴$EM// FN$.(内错角相等,两直线平行)
(2)如图,网格中每个小正方形的边长均为 1,$△ABC$的顶点均在小正方形的格点上.
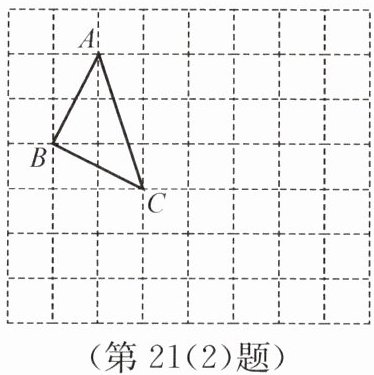
①将$△ABC$向下平移 3 个单位长度得到$△A_{1}B_{1}C_{1}$,画出$△A_{1}B_{1}C_{1}$;
②将$△ABC$绕点 C 顺时针旋转 90 度得到$△A_{2}B_{2}C_{2}$,画出$△A_{2}B_{2}C_{2}$.

已知:如图,在四边形 ABCD 中,ABCD,$∠B= ∠D$,点 E,F 分别在边 BC,AD 上,EM 平分$∠BEF$交 AB 于点 M,FN 平分$∠DFE$交 CD 于点 N.
求证:$EM// FN$.
证明:在四边形 ABCD 中,
∵$AB// CD$,(已知)
∴____,(两直线平行,同旁内角互补)
∵$∠B= ∠D$,(已知)
∴$∠C+∠D= 180^{\circ}$,(____)
∴____,(同旁内角互补,两直线平行)
∴____.(两直线平行,内错角相等)
∵EM 平分$∠BEF$,FN 平分$∠DFE$,(已知)
∴$∠1= \frac{1}{2}∠BEF$,$∠2= \frac{1}{2}∠DFE$,(____)
∴$∠1= ∠2$,(等量代换)
∴$EM// FN$.(内错角相等,两直线平行)
(2)如图,网格中每个小正方形的边长均为 1,$△ABC$的顶点均在小正方形的格点上.

①将$△ABC$向下平移 3 个单位长度得到$△A_{1}B_{1}C_{1}$,画出$△A_{1}B_{1}C_{1}$;
②将$△ABC$绕点 C 顺时针旋转 90 度得到$△A_{2}B_{2}C_{2}$,画出$△A_{2}B_{2}C_{2}$.
答案:
(1)①$\therefore ∠B+∠C=180^{\circ }$;②等量代换;③$AD// BC$;④$∠BEF=∠DFE$;⑤角平分线定义。
(2)
(1)①$\therefore ∠B+∠C=180^{\circ }$;②等量代换;③$AD// BC$;④$∠BEF=∠DFE$;⑤角平分线定义。
(2)

查看更多完整答案,请扫码查看


