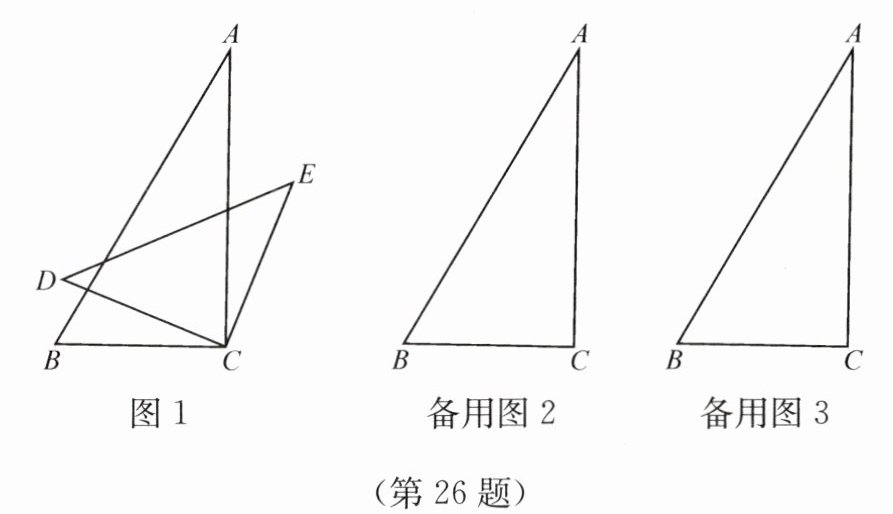
26. 如图 1,将一副三角板中的两个直角顶点 C 叠放在一起,其中$∠A= 30^{\circ },∠B= 60^{\circ },∠D= ∠E= 45^{\circ }$.
(1) 观察猜想,$∠BCD与∠ACE$的数量关系是
(2) 类比探究,若按住三角板 ABC 不动,顺时针绕直角顶点 C 转动三角形 DCE,试探究当$∠ACD等于多少度时CE// AB$,画出图形并简要说明理由.
(2)当$∠ACD$等于$60^{\circ}$或$120^{\circ}$时,$CE// AB$。理由如下:
① 如图1,当$∠ACD=60^{\circ}$时,因为$∠ACB=90^{\circ}$,所以$∠BCE=∠ACB - ∠ACE$,又因为$∠DCE=90^{\circ}$,$∠ACD=60^{\circ}$,所以$∠ACE=∠DCE - ∠ACD=90^{\circ}-60^{\circ}=30^{\circ}$,则$∠BCE=90^{\circ}-30^{\circ}=60^{\circ}$,因为$∠B=60^{\circ}$,所以$∠BCE=∠B$,所以$CE// AB$(内错角相等,两直线平行)。
② 如图2,当$∠ACD=120^{\circ}$时,因为$∠DCE=90^{\circ}$,所以$∠ACE=∠ACD - ∠DCE=120^{\circ}-90^{\circ}=30^{\circ}$,因为$∠A=30^{\circ}$,所以$∠ACE=∠A$,所以$CE// AB$(内错角相等,两直线平行)。
综上,当$∠ACD=60^{\circ}$或$120^{\circ}$时,$CE// AB$。
(1) 观察猜想,$∠BCD与∠ACE$的数量关系是
相等
;$∠BCE与∠ACD$的数量关系是互补
;(2) 类比探究,若按住三角板 ABC 不动,顺时针绕直角顶点 C 转动三角形 DCE,试探究当$∠ACD等于多少度时CE// AB$,画出图形并简要说明理由.

(2)当$∠ACD$等于$60^{\circ}$或$120^{\circ}$时,$CE// AB$。理由如下:
① 如图1,当$∠ACD=60^{\circ}$时,因为$∠ACB=90^{\circ}$,所以$∠BCE=∠ACB - ∠ACE$,又因为$∠DCE=90^{\circ}$,$∠ACD=60^{\circ}$,所以$∠ACE=∠DCE - ∠ACD=90^{\circ}-60^{\circ}=30^{\circ}$,则$∠BCE=90^{\circ}-30^{\circ}=60^{\circ}$,因为$∠B=60^{\circ}$,所以$∠BCE=∠B$,所以$CE// AB$(内错角相等,两直线平行)。
② 如图2,当$∠ACD=120^{\circ}$时,因为$∠DCE=90^{\circ}$,所以$∠ACE=∠ACD - ∠DCE=120^{\circ}-90^{\circ}=30^{\circ}$,因为$∠A=30^{\circ}$,所以$∠ACE=∠A$,所以$CE// AB$(内错角相等,两直线平行)。
综上,当$∠ACD=60^{\circ}$或$120^{\circ}$时,$CE// AB$。
答案:
(1)相等、互补;
(2)$60^{\circ}$或$120^{\circ}$
(1)相等、互补;
(2)$60^{\circ}$或$120^{\circ}$
27. 如图 1,在$△ABC$中,$∠ACB= 90^{\circ }$,点 P 在边 BC 上. 将点 P 绕点 B 按逆时针方向旋转一定角度$α(0^{\circ }<α<180^{\circ })得到点P'$,连接$AP',BP'作∠P'BC,∠ACB$的角平分线交于点 Q.
(1) 如图 2,若$α=90^{\circ }$,则$∠BCQ= $
(2) 如图 3,当点 P 恰好落在边 AB 上时,探索$∠A$、$∠BCQ$之间的关系,并说明理由.
(1) 如图 2,若$α=90^{\circ }$,则$∠BCQ= $
45
$^{\circ }$;(2) 如图 3,当点 P 恰好落在边 AB 上时,探索$∠A$、$∠BCQ$之间的关系,并说明理由.
$\angle BQC = 90^{\circ}+\frac{1}{2}\angle A$,理由如下:$\because BQ$平分$\angle ABC$,$CQ$平分$\angle ACB$,$\therefore\angle CBQ=\frac{1}{2}\angle ABC$,$\angle BCQ=\frac{1}{2}\angle ACB$,$\therefore\angle CBQ+\angle BCQ=\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB=\frac{1}{2}(\angle ABC+\angle ACB)$,在$\triangle ABC$中,$\angle A+\angle ABC+\angle ACB = 180^{\circ}$,$\therefore\angle ABC+\angle ACB = 180^{\circ}-\angle A$,$\therefore\angle CBQ+\angle BCQ=\frac{1}{2}(180^{\circ}-\angle A)$,在$\triangle BQC$中,$\angle CBQ+\angle BCQ+\angle BQC = 180^{\circ}$,$\therefore\angle BQC = 180^{\circ}-(\angle CBQ+\angle BCQ)=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle A)=90^{\circ}+\frac{1}{2}\angle A$
答案:
(1)$\because\alpha = 90^{\circ}$,$\therefore\angle P'BP = 90^{\circ}$,$\because BQ$平分$\angle P'BC$,$\therefore\angle QBC=\frac{1}{2}\angle P'BP = 45^{\circ}$,$\because CQ$平分$\angle ACB$,$\therefore\angle QCB=\frac{1}{2}\angle ACB = 45^{\circ}$,$\therefore\angle BQC = 180^{\circ}-(\angle QBC+\angle QCB)=90^{\circ}$;
(2)$\because BQ$平分$\angle ABC$,$CQ$平分$\angle ACB$,$\therefore\angle CBQ=\frac{1}{2}\angle ABC$,$\angle BCQ=\frac{1}{2}\angle ACB$,$\therefore\angle CBQ+\angle BCQ=\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB=\frac{1}{2}(\angle ABC+\angle ACB)$,在$\triangle ABC$中,$\angle A+\angle ABC+\angle ACB = 180^{\circ}$,$\therefore\angle ABC+\angle ACB = 180^{\circ}-\angle A$,$\therefore\angle CBQ+\angle BCQ=\frac{1}{2}(180^{\circ}-\angle A)$,在$\triangle BQC$中,$\angle CBQ+\angle BCQ+\angle BQC = 180^{\circ}$,$\therefore\angle BQC = 180^{\circ}-(\angle CBQ+\angle BCQ)=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle A)=90^{\circ}+\frac{1}{2}\angle A$.
(1)$\because\alpha = 90^{\circ}$,$\therefore\angle P'BP = 90^{\circ}$,$\because BQ$平分$\angle P'BC$,$\therefore\angle QBC=\frac{1}{2}\angle P'BP = 45^{\circ}$,$\because CQ$平分$\angle ACB$,$\therefore\angle QCB=\frac{1}{2}\angle ACB = 45^{\circ}$,$\therefore\angle BQC = 180^{\circ}-(\angle QBC+\angle QCB)=90^{\circ}$;
(2)$\because BQ$平分$\angle ABC$,$CQ$平分$\angle ACB$,$\therefore\angle CBQ=\frac{1}{2}\angle ABC$,$\angle BCQ=\frac{1}{2}\angle ACB$,$\therefore\angle CBQ+\angle BCQ=\frac{1}{2}\angle ABC+\frac{1}{2}\angle ACB=\frac{1}{2}(\angle ABC+\angle ACB)$,在$\triangle ABC$中,$\angle A+\angle ABC+\angle ACB = 180^{\circ}$,$\therefore\angle ABC+\angle ACB = 180^{\circ}-\angle A$,$\therefore\angle CBQ+\angle BCQ=\frac{1}{2}(180^{\circ}-\angle A)$,在$\triangle BQC$中,$\angle CBQ+\angle BCQ+\angle BQC = 180^{\circ}$,$\therefore\angle BQC = 180^{\circ}-(\angle CBQ+\angle BCQ)=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle A)=90^{\circ}+\frac{1}{2}\angle A$.
查看更多完整答案,请扫码查看


