21. (1)已知:$ \overline{abcd} $是一个四位数,$ a + b + c + d $可以被9整除.
求证:$ \overline{abcd} $这个四位数可以被9整除.
(2)已知:m是正整数,且$ m^{2} $是奇数.
求证:m是奇数.
求证:$ \overline{abcd} $这个四位数可以被9整除.
(2)已知:m是正整数,且$ m^{2} $是奇数.
求证:m是奇数.
答案:
(1) 证明:$\because \overline{a b c d}=1000 a+100 b+10 c+d=(a+b+c+d)+(999 a+99 b+9 c)=(a+b+c+d)+9(111 a+11 b+c)$ 又 $\because a+b+c+d$ 可以被 9 整除,$\therefore \overline{a b c d}$ 这个四位数可以被 9 整除.
(2) 证明:假设 $m$ 是偶数,则 $m=2 n$($n$ 为正整数).$\therefore m^{2}=(2 n)^{2}=4n^{2}$. 这时可知 $m^{2}$ 为偶数. 这与已知 $m^{2}$ 是奇数相矛盾,$\therefore$ 假设 $m$ 是偶数不成立. $\therefore m$ 是奇数.
(1) 证明:$\because \overline{a b c d}=1000 a+100 b+10 c+d=(a+b+c+d)+(999 a+99 b+9 c)=(a+b+c+d)+9(111 a+11 b+c)$ 又 $\because a+b+c+d$ 可以被 9 整除,$\therefore \overline{a b c d}$ 这个四位数可以被 9 整除.
(2) 证明:假设 $m$ 是偶数,则 $m=2 n$($n$ 为正整数).$\therefore m^{2}=(2 n)^{2}=4n^{2}$. 这时可知 $m^{2}$ 为偶数. 这与已知 $m^{2}$ 是奇数相矛盾,$\therefore$ 假设 $m$ 是偶数不成立. $\therefore m$ 是奇数.
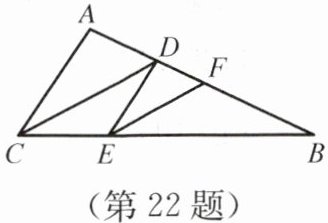
22. 如图所示,已知CD平分$ \angle ACB $,$ AC // DE $,$ CD // EF $,求证:EF平分$ \angle DEB $.

答案:
证明:$\because CD$ 平分 $\angle A C B$,$\therefore \angle A C D=\angle D C B$.$\because A C // D E$,$\therefore \angle A C D=\angle C D E$.$\because D C // E F$,$\therefore \angle C D E=\angle D E F$,$\angle D C B=\angle F E B$.$\therefore \angle D E F=\angle F E B$.$\therefore E F$ 平分 $\angle D E B$.
查看更多完整答案,请扫码查看


