第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 计算:
(1)$(π-3.14)^{0}+(\frac {1}{2})^{-1}-|-2|-(-1)^{2024}$ (2)$201×199$(简便计算)
(3)$(x-2y)^{2}-(x+4y)(3x+y)$
(1)$(π-3.14)^{0}+(\frac {1}{2})^{-1}-|-2|-(-1)^{2024}$ (2)$201×199$(简便计算)
(3)$(x-2y)^{2}-(x+4y)(3x+y)$
答案:
解:(1)原式$=1+2-2-1$
$=0$
(2)原式$=(200+1)×(200-1)$
$=200^{2}-1$
$=39999$
(3)原式$=x^{2}-4xy+4y^{2}-(3x^{2}+xy+12xy+4y^{2})$
$=x^{2}-4xy+4y^{2}-3x^{2}-xy-12xy-4y^{2}$
$=-2x^{2}-17xy$
$=0$
(2)原式$=(200+1)×(200-1)$
$=200^{2}-1$
$=39999$
(3)原式$=x^{2}-4xy+4y^{2}-(3x^{2}+xy+12xy+4y^{2})$
$=x^{2}-4xy+4y^{2}-3x^{2}-xy-12xy-4y^{2}$
$=-2x^{2}-17xy$
2. 在一个不透明的盒子里装有规格相同、颜色不同的黑、白两种球共 20 个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下图是“摸到白球”的频率折线统计图。
(1)请估计:当摸球次数很大时,摸到白球的频率将会接近
(2)试估算盒子里黑、白两种颜色的球各有多少个。
解:白色球:$20×0.5=10$(个),黑色球:$20-10=10$(个);
答:估算盒子里白、黑两种颜色的球分别有10个、10个;
(3)在(2)的条件下,如果要使摸到白球的概率为$\frac {3}{5}$,需要往盒子里再放入多少个白球?
解:设需要往盒子里再放入x个白球;
根据题意得:$\frac {10+x}{20+x}=\frac {3}{5}$,
解得:$x=5$;
答:需要往盒子里再放入5个白球。
(1)请估计:当摸球次数很大时,摸到白球的频率将会接近
0.50
。(2)试估算盒子里黑、白两种颜色的球各有多少个。
解:白色球:$20×0.5=10$(个),黑色球:$20-10=10$(个);
答:估算盒子里白、黑两种颜色的球分别有10个、10个;
(3)在(2)的条件下,如果要使摸到白球的概率为$\frac {3}{5}$,需要往盒子里再放入多少个白球?
解:设需要往盒子里再放入x个白球;
根据题意得:$\frac {10+x}{20+x}=\frac {3}{5}$,
解得:$x=5$;
答:需要往盒子里再放入5个白球。
答案:
解:(1)0.50;
(2)白色球:$20×0.5=10$(个),黑色球:$20-10=10$(个);
答:估算盒子里白、黑两种颜色的球分别有10个、10个;
(3)设需要往盒子里再放入x个白球;
根据题意得:$\frac {10+x}{20+x}=\frac {1}{2}$,
解得:$x=5$;
答:需要往盒子里再放入5个白球。
(2)白色球:$20×0.5=10$(个),黑色球:$20-10=10$(个);
答:估算盒子里白、黑两种颜色的球分别有10个、10个;
(3)设需要往盒子里再放入x个白球;
根据题意得:$\frac {10+x}{20+x}=\frac {1}{2}$,
解得:$x=5$;
答:需要往盒子里再放入5个白球。
3. 如图,在$△ABC$中,$DE// BC$交 AB 和 AC 于点 D 和 E。
(1)请用无刻度的直尺和圆规作出$∠B$的平分线(保留作图痕迹,不写作法)。
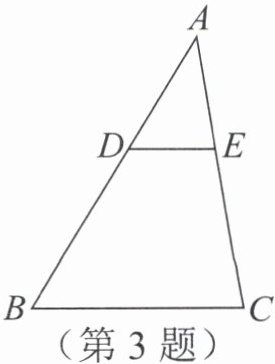
(2)若(1)中所作的角平分线与 DE 的延长线交于点 F,试判断$△DBF$的形状并说明理由。
解:(1)如图,BF即为所求。

(2)$\triangle DBF$为等腰三角形。
理由:∵BF为$∠ABC$的平分线,$\therefore ∠ABF=∠CBF$。
$\because DE// BC,\therefore ∠DFB=∠CBF$。
$\therefore ∠ABF=∠DFB$。$\therefore DB=DF$。
$\therefore \triangle DBF$为等腰三角形。
(1)请用无刻度的直尺和圆规作出$∠B$的平分线(保留作图痕迹,不写作法)。

(2)若(1)中所作的角平分线与 DE 的延长线交于点 F,试判断$△DBF$的形状并说明理由。
解:(1)如图,BF即为所求。

(2)$\triangle DBF$为等腰三角形。
理由:∵BF为$∠ABC$的平分线,$\therefore ∠ABF=∠CBF$。
$\because DE// BC,\therefore ∠DFB=∠CBF$。
$\therefore ∠ABF=∠DFB$。$\therefore DB=DF$。
$\therefore \triangle DBF$为等腰三角形。
答案:
解:(1)如图,BF即为所求。

(2)$\triangle DBF$为等腰三角形。
理由:
∵BF为$∠ABC$的平分线,$\therefore ∠ABF=∠CBF$。
$\because DE// BC,\therefore ∠DFB=∠CBF$。
$\therefore ∠ABF=∠DFB$。$\therefore DB=DF$。
$\therefore \triangle DBF$为等腰三角形。
解:(1)如图,BF即为所求。

(2)$\triangle DBF$为等腰三角形。
理由:
∵BF为$∠ABC$的平分线,$\therefore ∠ABF=∠CBF$。
$\because DE// BC,\therefore ∠DFB=∠CBF$。
$\therefore ∠ABF=∠DFB$。$\therefore DB=DF$。
$\therefore \triangle DBF$为等腰三角形。
查看更多完整答案,请扫码查看


