《2025年暑假生活指导七年级山东教育出版社》

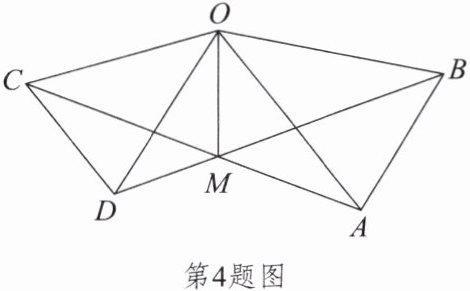
4. 如图,在$\triangle OAB和\triangle OCD$中,$OA = OB$,$OC = OD$,$OA\gt OC$,$\angle AOB= \angle COD = 40^{\circ}$,连接$AC$,$BD交于点M$,连接$OM$。下列结论：①$AC = BD$；②$\angle AMB = 40^{\circ}$；③$OM平分\angle BOC$；④$MO平分\angle BMC$。其中正确结论的个数为( )。


A.4
B.3
C.2
D.1

答案： 【解析】：$\because\angle AOB=\angle COD$，
$\therefore\angle AOC=\angle BOD$，
$\because OA=OB$，$OC=OD$，
在$\triangle AOC$和$\triangle BOD$中，
$\begin{cases}OA=OB\\\angle AOC=\angle BOD\\OC=OD\end{cases}$
$\therefore \triangle AOC\cong\triangle BOD(SAS)$，
$\therefore AC=BD$，$\angle OAC=\angle OBD$，
由三角形的外角性质得：
$\angle AMB=\angle OAC+\angle OBA=\angle OBD+\angle OBA=\angle AOB=40^{\circ}$，
作$OG\perp MC$于$G$，$OH\perp MB$于$H$，
$\therefore\angle OGC=\angle OHD=90^{\circ}$，
在$\triangle OCG$和$\triangle ODH$中，
$\begin{cases}\angle OGC=\angle OHD\\\angle COG=\angle DOH\\OC=OD\end{cases}$
$\therefore\triangle OCG\cong\triangle ODH(AAS)$，
$\therefore OG=OH$，
$\therefore$点$O$在$\angle BMC$的平分线上，
即$MO$平分$\angle BMC$，
但$OM$不一定平分$\angle BOC$，
$\therefore$①②④正确，③错误。
【答案】：B

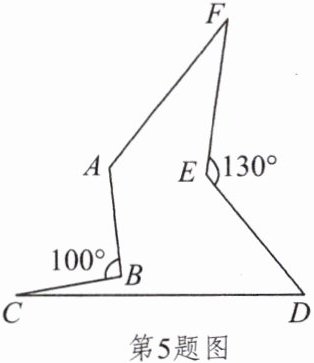
5. 如图,$\angle ABC = 100^{\circ}$,$\angle DEF = 130^{\circ}$,则$\angle A+\angle C+\angle D+\angle F$的度数为______。

答案： 230°

6. 材料阅读：如图①所示的图形,像我们常见的学习用品——圆规。我们不妨把这样的图形叫作“规形图”。
解决问题：
(1)观察“规形图”,试探究$\angle BDC与\angle A$,$\angle B$,$\angle C$之间的数量关系,并说明理由；
(2)请你直接利用以上结论,解决以下两个问题：
①如图②,把一个三角尺$DEF放置在\triangle ABC$上,使三角尺的两条直角边$DE$,$DF恰好经过点B$,$C$,若$\angle A = 40^{\circ}$,则$\angle ABD+\angle ACD= $______。

②如图③,$BD平分\angle ABP$,$CD平分\angle ACP$,若$\angle A = 40^{\circ}$,$\angle BPC = 130^{\circ}$,求$\angle BDC$的度数。

答案： 【解析】：
(1) 根据“规形图”的性质，$\angle BDC = \angle A + \angle B + \angle C$。
理由如下：
在三角形$ABD$中，
$\angle BDE = \angle A + \angle B$（三角形的一个外角等于与它不相邻的两个内角的和），
在三角形$CDE$中，
$\angle EDC= \angle EDC + \angle C$，
$\angle BDC = \angle BDE + \angle EDC = \angle A + \angle B + \angle C$。
(2) ① 利用
(1)的结论：
$\angle D = \angle A + \angle ABD + \angle ACD$，
$\angle D = 90^\circ$，
$\angle A = 40^\circ$，
所以：
$\angle ABD + \angle ACD = 90^\circ - 40^\circ = 50^\circ$。
② 利用
(1)的结论：
$\angle BPC = \angle A + \angle ABP + \angle ACP$，
$\angle BDC = \angle A + \angle ABD + \angle ACD$，
因为$BD$平分$\angle ABP$，$CD$平分$\angle ACP$，
所以：
$\angle ABD = \frac{1}{2} \angle ABP$，
$\angle ACD = \frac{1}{2} \angle ACP$，
$\angle BPC = 130^\circ$，
$\angle A = 40^\circ$，
$\angle ABP + \angle ACP = 130^\circ - 40^\circ = 90^\circ$，
$\angle BDC = 40^\circ + \frac{1}{2} × 90^\circ = 85^\circ$。
【答案】：
(1) $\angle BDC = \angle A + \angle B + \angle C$
(2) ① $50^\circ$
② $85^\circ$