第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
10. 甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价$20\%$,后又降价$10\%$;乙超市连续两次降价$15\%$;丙超市一次降价$30\%$。那么顾客到哪家超市购买这种商品更合算( )。
A.甲
B.乙
C.丙
D.一样
A.甲
B.乙
C.丙
D.一样
答案:
【解析】:
设商品原价为$M$,
甲超市先降价$20\%$,后又降价$10\%$,
则降价后的价格为:$M × (1 - 20\%) × (1 - 10\%) = M × 0.8 × 0.9 = 0.72M$,
乙超市连续两次降价$15\%$,
则降价后的价格为:$M × (1 - 15\%) × (1 - 15\%) = M × 0.85 × 0.85 = 0.7225M$,
丙超市一次降价$30\%$,
则降价后的价格为:$M × (1 - 30\%) = 0.7M$,
比较三家超市降价后的价格,$0.7M \lt 0.72M \lt 0.7225M$,
可以看出丙超市的价格最低。
【答案】:C
设商品原价为$M$,
甲超市先降价$20\%$,后又降价$10\%$,
则降价后的价格为:$M × (1 - 20\%) × (1 - 10\%) = M × 0.8 × 0.9 = 0.72M$,
乙超市连续两次降价$15\%$,
则降价后的价格为:$M × (1 - 15\%) × (1 - 15\%) = M × 0.85 × 0.85 = 0.7225M$,
丙超市一次降价$30\%$,
则降价后的价格为:$M × (1 - 30\%) = 0.7M$,
比较三家超市降价后的价格,$0.7M \lt 0.72M \lt 0.7225M$,
可以看出丙超市的价格最低。
【答案】:C
11. 如图,$AD是\triangle ABC中\angle BAC$的角平分线,$DE\perp AB于点E$,$S_{\triangle ABC}= 7$,$DE = 2$,$AB = 4$,则$AC$长是( )。

A.3
B.4
C.6
D.5

A.3
B.4
C.6
D.5
答案:
【解析】:
由于 $AD$ 是 $\triangle ABC$ 中 $\angle BAC$ 的角平分线,且 $DE \perp AB$ 于点 $E$,
根据角平分线的性质,点 $D$ 到 $AB$ 和 $AC$ 的距离是相等的。
已知 $DE = 2$,
因此点 $D$ 到 $AC$ 的距离也是 $2$。
设点 $D$ 到 $AC$ 的垂足为 $F$,则 $DF = 2$。
根据三角形的面积公式,有:
$S_{\triangle ABC} = S_{\triangle ABD} + S_{\triangle ACD}$
$= \frac{1}{2} × AB × DE + \frac{1}{2} × AC × DF$
$= \frac{1}{2} × 4 × 2 + \frac{1}{2} × AC × 2$
$= 4 + AC$
已知 $S_{\triangle ABC} = 7$,代入上式得:
$4 + AC = 7$
解得 $AC = 3$。
【答案】:A
由于 $AD$ 是 $\triangle ABC$ 中 $\angle BAC$ 的角平分线,且 $DE \perp AB$ 于点 $E$,
根据角平分线的性质,点 $D$ 到 $AB$ 和 $AC$ 的距离是相等的。
已知 $DE = 2$,
因此点 $D$ 到 $AC$ 的距离也是 $2$。
设点 $D$ 到 $AC$ 的垂足为 $F$,则 $DF = 2$。
根据三角形的面积公式,有:
$S_{\triangle ABC} = S_{\triangle ABD} + S_{\triangle ACD}$
$= \frac{1}{2} × AB × DE + \frac{1}{2} × AC × DF$
$= \frac{1}{2} × 4 × 2 + \frac{1}{2} × AC × 2$
$= 4 + AC$
已知 $S_{\triangle ABC} = 7$,代入上式得:
$4 + AC = 7$
解得 $AC = 3$。
【答案】:A
1. 如图,$AD是\triangle ABC$的中线,分别过点$B$,$C作AD$的垂线,垂足为$E$,$F$,试判断$BE与CF$的关系,并说明理由。


答案:
【解析】:
根据题意,$AD$是$\triangle ABC$的中线,因此$D$是$BC$的中点,即$BD = DC$。
过点$B$和$C$分别作$AD$的垂线,垂足分别为$E$和$F$。
由于$AD$是中线,$\triangle ABD$和$\triangle ACD$的面积相等,且$BD = DC$,所以$BE$和$CF$分别是$\triangle ABD$和$\triangle ACD$的高。
根据三角形面积公式,面积相等且底边相等,则高也相等。因此$BE = CF$。
同时,$BE$和$CF$都垂直于$AD$,所以$BE // CF$。
综合以上分析,$BE$与$CF$的关系是:$BE = CF$且$BE // CF$。
【答案】:$BE = CF$,$BE // CF$
根据题意,$AD$是$\triangle ABC$的中线,因此$D$是$BC$的中点,即$BD = DC$。
过点$B$和$C$分别作$AD$的垂线,垂足分别为$E$和$F$。
由于$AD$是中线,$\triangle ABD$和$\triangle ACD$的面积相等,且$BD = DC$,所以$BE$和$CF$分别是$\triangle ABD$和$\triangle ACD$的高。
根据三角形面积公式,面积相等且底边相等,则高也相等。因此$BE = CF$。
同时,$BE$和$CF$都垂直于$AD$,所以$BE // CF$。
综合以上分析,$BE$与$CF$的关系是:$BE = CF$且$BE // CF$。
【答案】:$BE = CF$,$BE // CF$
2. 先化简,再求值:$(x - 1)(x + 1)-x(x - 3)$,其中$x = 3$。
答案:
【解析】:首先,利用平方差公式化简$(x - 1)(x + 1)$,得到$x^2 - 1$。然后,展开$x(x - 3)$,得到$x^2 - 3x$。接下来,将两个结果相减:$(x^2 - 1) - (x^2 - 3x) = x^2 - 1 - x^2 + 3x = 3x - 1$。最后,把$x = 3$代入化简后的式子$3x - 1$,计算可得$3×3 - 1 = 8$。
【答案】:8
【答案】:8
3. 已知$x^{m}=5$,$x^{n}=7$,求$x^{2m + n}$的值。
答案:
【解析】:
已知 $x^{m} = 5$ 和 $x^{n} = 7$,
要求 $x^{2m + n}$ 的值。
根据同底数幂的乘法法则,有:
$x^{2m + n} = x^{2m} \cdot x^{n}$
再根据幂的乘方法则,可以将 $x^{2m}$ 转化为 $(x^{m})^{2}$,即:
$x^{2m + n} = (x^{m})^{2} \cdot x^{n}$
代入已知的 $x^{m} = 5$ 和 $x^{n} = 7$,得:
$x^{2m + n} = 5^{2} × 7 = 25 × 7 = 175$
【答案】:175
已知 $x^{m} = 5$ 和 $x^{n} = 7$,
要求 $x^{2m + n}$ 的值。
根据同底数幂的乘法法则,有:
$x^{2m + n} = x^{2m} \cdot x^{n}$
再根据幂的乘方法则,可以将 $x^{2m}$ 转化为 $(x^{m})^{2}$,即:
$x^{2m + n} = (x^{m})^{2} \cdot x^{n}$
代入已知的 $x^{m} = 5$ 和 $x^{n} = 7$,得:
$x^{2m + n} = 5^{2} × 7 = 25 × 7 = 175$
【答案】:175
1. 如图:小刚站在河边的$A$点处,在河的对面(小刚的正北方向)的$B$处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树$C$处,接着再向前走了30步到达$D$处,然后他左转$90^{\circ}$直行,当小刚看到电线塔、树与自己现处的位置$E$在一条直线时,他共走了140步。(1)根据题意,画出示意图;(2)如果小刚一步大约50厘米,估计小刚在点$A$处时他与电线塔的距离,并说明理由。


答案:
(1)
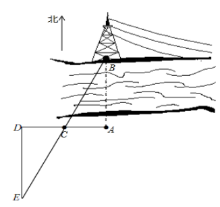
(2)由题意,小刚共走了140步,从A到C到D到E的步数为AC+CD+DE=30+30+DE=140,解得DE=80步。因为AB⊥AD,ED⊥AD,所以∠BAC=∠EDC=90°,又∠ACB=∠DCE(对顶角相等),所以△ABC∽△DEC(两角对应相等的两个三角形相似)。根据相似三角形对应边成比例,有AB/DE=AC/CD,已知AC=30步,CD=30步,所以AC=CD,因此AB=DE=80步。一步约50厘米,AB=80×50=4000厘米=40米。
(1)

(2)由题意,小刚共走了140步,从A到C到D到E的步数为AC+CD+DE=30+30+DE=140,解得DE=80步。因为AB⊥AD,ED⊥AD,所以∠BAC=∠EDC=90°,又∠ACB=∠DCE(对顶角相等),所以△ABC∽△DEC(两角对应相等的两个三角形相似)。根据相似三角形对应边成比例,有AB/DE=AC/CD,已知AC=30步,CD=30步,所以AC=CD,因此AB=DE=80步。一步约50厘米,AB=80×50=4000厘米=40米。
2. 某中学为筹备校庆活动,准备印制一批校庆纪念册。该纪念册每册需要10张8开大小的纸,其中4张为彩页,6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩页300元/张,黑白页50元/张;印刷费与印数的关系见下表。
| 印数$a$(单位:千册) | $1\leqslant a\lt5$ | $5\leqslant a\lt10$ |
| 彩色(单位:元/张) | $2.2$ | $2.0$ |
| 黑白(单位:元/张) | $0.7$ | $0.6$ |
(1)印制这批纪念册的制版费为多少元;
(2)若印制2000册,则共需多少费用?
| 印数$a$(单位:千册) | $1\leqslant a\lt5$ | $5\leqslant a\lt10$ |
| 彩色(单位:元/张) | $2.2$ | $2.0$ |
| 黑白(单位:元/张) | $0.7$ | $0.6$ |
(1)印制这批纪念册的制版费为多少元;
(2)若印制2000册,则共需多少费用?
答案:
【解析】:
(1) 制版费的计算:
彩页的制版费为:$4 × 300 = 1200$( 元),
黑白页的制版费为:$6 × 50 = 300$( 元),
因此,印制这批纪念册的制版费为:$1200 + 300 = 1500$( 元),
(2) 印刷费的计算(印制2000册,即$a=2$千册,所以印刷费按$1\leqslant a\lt5$的标准计算):
每册纪念册有4张彩页和6张黑白页,所以:
彩页的印刷费为:$2000 × 4 × 2.2 = 17600$( 元),
黑白页的印刷费为:$2000 × 6 × 0.7 = 8400$( 元),
因此,印制2000册纪念册的总费用(包括制版费和印刷费)为:$1500 + 17600 + 8400 = 27500$( 元),
【答案】:
(1) 1500元;
(2) 27500元。
(1) 制版费的计算:
彩页的制版费为:$4 × 300 = 1200$( 元),
黑白页的制版费为:$6 × 50 = 300$( 元),
因此,印制这批纪念册的制版费为:$1200 + 300 = 1500$( 元),
(2) 印刷费的计算(印制2000册,即$a=2$千册,所以印刷费按$1\leqslant a\lt5$的标准计算):
每册纪念册有4张彩页和6张黑白页,所以:
彩页的印刷费为:$2000 × 4 × 2.2 = 17600$( 元),
黑白页的印刷费为:$2000 × 6 × 0.7 = 8400$( 元),
因此,印制2000册纪念册的总费用(包括制版费和印刷费)为:$1500 + 17600 + 8400 = 27500$( 元),
【答案】:
(1) 1500元;
(2) 27500元。
查看更多完整答案,请扫码查看


