《2025年暑假生活指导七年级山东教育出版社》

3. 已知三角形两边的长分别为1、5,第三边长为整数,则第三边的长为______。

答案： 【解析】：设第三边长为$x$。
根据三角形的性质，两边之和大于第三边，即：
$1 + 5 ＞ x$
$x ＜ 6$
同时，两边之差小于第三边，即：
$5 - 1 ＜ x$
$x ＞ 4$
综合以上两个不等式，得到第三边$x$的取值范围为：
$4 ＜ x ＜ 6$
由于题目要求第三边长为整数，因此在这个范围内只有$x = 5$满足条件。
【答案】：5

4. 将一块$60^{\circ}的直角三角板DEF放置在45^{\circ}的直角三角板ABC$上,移动三角板$DEF使两条直角边DE$、$DF恰分别经过B$、$C$两点,若$EF// BC$,则$\angle ABD= $______$^{\circ}$。

答案： 【解析】：
因$EF// BC$，
则$\angle DBC=\angle DFB$。
由于$\angle DFB=180^\circ-\angle FDC-\angle FCB=180^\circ-90^\circ-60^\circ=30^\circ$，
所以$\angle DBC=30^\circ$。
在$\triangle ABC$中，$\angle ABC=45^\circ$，
所以$\angle ABD=\angle ABC-\angle DBC=45^\circ-30^\circ=15^\circ$。
【答案】：$15^\circ$

1. 已知：如图,$\angle BAC= \angle DAM$,$AB = AN$,$AD = AM$。求证：$\angle B= \angle ANM$。

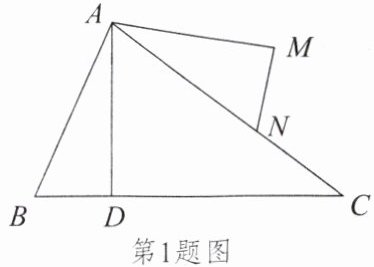
答案： 【解析】：
首先，根据题目条件，$\angle BAC=\angle DAM$，
通过等量代换可得：$\angle BAC-\angle DAC=\angle DAM-\angle DAC$，
即：$\angle BAD=\angle NAM$。
在$\triangle ABD$和$\triangle ANM$中：
$AB=AN$，
$\angle BAD=\angle NAM$，
$AD=AM$。
由此，根据SAS（边-角-边）定理，可以得出$\triangle ABD\cong\triangle ANM$。
由于全等三角形对应角相等，
因此，$\angle B=\angle ANM$。
【答案】：
$\angle B=\angle ANM$

2. 如图所示,折叠一个宽度相等的纸条,求$\angle 1$的度数。

答案： 【解析】：因为纸条的上下两边是平行的，即 $AB // CD$，根据两直线平行，同旁内角互补，所以$\angle AEF + \angle CFE = 180^\circ$。已知$\angle CFE = 80^\circ$，则$\angle AEF = 180^\circ - 80^\circ = 100^\circ$。
由折叠的性质可知，折叠前后对应角相等，所以$\angle 2 = \angle 3$。又因为$\angle AEF = \angle 2 + \angle 3$，即$100^\circ = 2\angle 2$，解得$\angle 2 = 50^\circ$。
由于$AB // CD$，根据两直线平行，内错角相等，可得$\angle 1 = \angle 2 = 50^\circ$。
【答案】：50°

1. 将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,求$\angle 1+\angle 2$的度数。

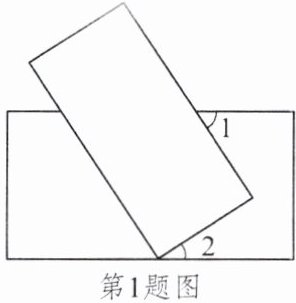
答案： 【解析】：
设矩形上边交点为$E$，过点$E$作$EF$平行于$CD$。
$AB// CD$，$EF// CD$，所以$AB// EF$。
由于两直线平行，同旁内角互补，
所以$\angle 1+\angle FEC=180^\circ$。
又因为$AD// BC$，$EF// BC$，所以$EF// AD$。
由于两直线平行，内错角相等，
所以$\angle 2=\angle FEC$。
$\angle 1+\angle 2=\angle 1+\angle FEC=180^\circ-90^\circ=90^\circ$。
【答案】：$90^\circ$

2. 王强同学用10块高度都是$2cm$的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板($AC = BC$,$\angle ACB = 90^{\circ}$),点$C在DE$上,点$A和B$分别与木墙的顶端重合,求两堵木墙之间的距离。

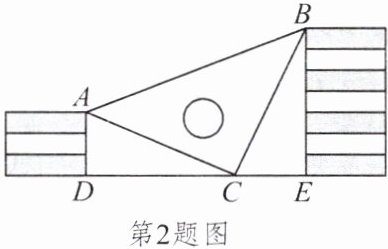
答案： 【解析】：设两堵木墙之间的距离为$CD + CE = x$。已知每个小木块高度为$2cm$，假设左边木墙由$m$块木块组成，右边由$n$块组成（根据题意及图形可推测$m=3$，$n=7$，此处需结合图形信息，实际解题时通过全等三角形证明得出）。
因为$\angle ACB = 90^{\circ}$，所以$\angle ACD + \angle BCE = 90^{\circ}$。又因为$AD \perp DE$，$BE \perp DE$，所以$\angle ADC = \angle CEB = 90^{\circ}$，$\angle ACD + \angle CAD = 90^{\circ}$，故$\angle CAD = \angle BCE$。
在$\triangle ADC$和$\triangle CEB$中，$\begin{cases} \angle ADC = \angle CEB \\ \angle CAD = \angle BCE \\ AC = BC \end{cases}$，所以$\triangle ADC \cong \triangle CEB(AAS)$。
则$AD = CE$，$CD = BE$。左边木墙高度$AD = 3×2 = 6cm$，右边木墙高度$BE = 7×2 = 14cm$，所以$CE = 6cm$，$CD = 14cm$，两墙距离$DE = CD + CE = 14 + 6 = 20cm$。
【答案】：20cm

3. 如图所示,潜望镜中的两个镜子是平行放置的,光线经过镜子反射后,$\angle 1= \angle 2$,$\angle 3= \angle 4$,请你解释为什么开始进入潜望镜的光线和最后离开潜望镜的光线是平行的。

答案： 【解析】：
因为两个镜子是平行放置的，
根据两直线平行，同旁内角互补的性质，
所以$\angle 2+\angle 3=180^\circ$，
又因为$\angle 1=\angle 2$，$\angle 3=\angle 4$，
所以$\angle 1+\angle 2+\angle 3+\angle 4=180^\circ×2=360^\circ$，
则$\angle 5+\angle 6=360^\circ-(\angle 1+\angle 2+\angle 3+\angle 4)+(\angle 2+\angle 3)=180^\circ$，
根据同旁内角互补，两直线平行，
所以$AB// CD$，
即开始进入潜望镜的光线和最后离开潜望镜的光线是平行的。
【答案】：因为潜望镜中镜子平行，$\angle 2+\angle 3=180^\circ$，且$\angle 1=\angle 2$，$\angle 3=\angle 4$，所以$\angle 5+\angle 6=180^\circ$，两光线平行。