《2025年暑假生活指导七年级山东教育出版社》

2. 下面四个图标中是轴对称图形的是( )。

答案： D

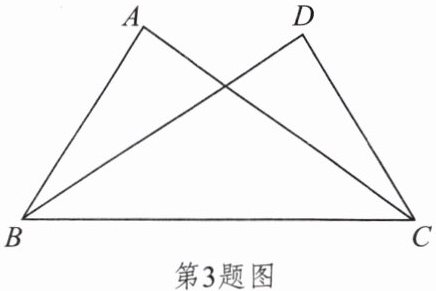
3. 如图,已知$\angle ABC= \angle DCB$,下列所给条件不能证明$\triangle ABC\cong\triangle DCB$的是( )。

A.$\angle A= \angle D$
B.$AB = DC$
C.$\angle ACB= \angle DBC$
D.$AC = BD$

答案： 【解析】：已知$\angle ABC = \angle DCB$，且$BC$为$\triangle ABC$和$\triangle DCB$的公共边（即$BC = CB$）。
选项A：若$\angle A=\angle D$，结合已知$\angle ABC = \angle DCB$和公共边$BC = CB$，可根据“AAS”（两角及其中一角的对边对应相等）证明$\triangle ABC\cong\triangle DCB$。
选项B：若$AB = DC$，结合已知$\angle ABC = \angle DCB$和公共边$BC = CB$，可根据“SAS”（两边及其夹角对应相等）证明$\triangle ABC\cong\triangle DCB$。
选项C：若$\angle ACB=\angle DBC$，结合已知$\angle ABC = \angle DCB$和公共边$BC = CB$，可根据“ASA”（两角及其夹边对应相等）证明$\triangle ABC\cong\triangle DCB$。
选项D：若$AC = BD$，此时为“SSA”（两边及其中一边的对角对应相等），而“SSA”不能作为判定三角形全等的依据，无法证明$\triangle ABC\cong\triangle DCB$。
【答案】：D

4. 如图,直线$a// b$,$AC\perp AB$,$AC交直线b于点C$,$\angle 1 = 65^{\circ}$,则$\angle 2$的度数是( )。


A.$65^{\circ}$
B.$50^{\circ}$
C.$35^{\circ}$
D.$25^{\circ}$

答案： 【解析】：
通过点$A$作直线$d$平行于直线$b$，则直线$d// a// b$，
所以$\angle 2=\angle 3$，$\angle 1=\angle 4$，
因为$AC\perp AB$，
所以$\angle BAC=90^\circ$，
所以$\angle 2+\angle 1=\angle 3+\angle 4=90^\circ$，
又因为$\angle 1 = 65^\circ$，
所以$\angle 2=90^\circ-65^\circ=25^\circ$。
【答案】：D

5. 下列运算正确的是( )。

A.$a^{2}\cdot a^{4}= a^{8}$
B.$a^{4}-a^{3}= a$
C.$(a^{2})^{3}= a^{5}$
D.$a^{4}÷ a^{2}= a^{2}$

答案： 【解析】：
A选项：根据同底数幂的乘法法则，有 $a^{m} \cdot a^{n} = a^{m+n}$。
所以 $a^{2} \cdot a^{4} = a^{2+4} = a^{6}$，与A选项中的 $a^{8}$ 不符，所以A选项错误。
B选项：$a^{4}$ 和 $a^{3}$ 是不同的项，它们之间不能直接进行合并，所以 $a^{4} - a^{3}$ 无法简化为 $a$，B选项错误。
C选项：根据幂的乘方法则，有 $(a^{m})^{n} = a^{m × n}$。
所以 $(a^{2})^{3} = a^{2 × 3} = a^{6}$，与C选项中的 $a^{5}$ 不符，所以C选项错误。
D选项：根据同底数幂的除法法则，有 $a^{m} ÷ a^{n} = a^{m-n}$。
所以 $a^{4} ÷ a^{2} = a^{4-2} = a^{2}$，与D选项中的 $a^{2}$ 符合，所以D选项正确。
【答案】：D

6. 下列运算中,结果是$a^{6}$的是( )。

A.$a^{2}\cdot a^{3}$
B.$a^{12}÷ a^{2}$
C.$(a^{3})^{3}$
D.$(-a)^{6}$

答案： 【解析】：
对于选项A，使用指数的乘法法则，同底数幂相乘，底数不变，指数相加，即 $a^{m} \cdot a^{n} = a^{m+n}$，所以 $a^{2} \cdot a^{3} = a^{2+3} = a^{5}$，不等于 $a^{6}$，故A选项错误。
对于选项B，使用指数的除法法则，同底数幂相除，底数不变，指数相减，即 $a^{m} {÷} a^{n} = a^{m-n}$，所以 $a^{12} {÷} a^{2} = a^{12-2} = a^{10}$，不等于 $a^{6}$，故B选项错误。
对于选项C，使用幂的幂的运算法则，幂的幂，底数不变，指数相乘，即 $(a^{m})^{n} = a^{m × n}$，所以 $(a^{3})^{3} = a^{3 × 3} = a^{9}$，不等于 $a^{6}$，故C选项错误。
对于选项D，$(-a)^{6}$ 表示 $-a$ 的六次方。由于负数的偶数次方结果为正，所以 $(-a)^{6} = a^{6}$，故D选项正确。
【答案】：D

7. 已知实数$a$,$b满足a + b = 3$,$a - b = 5$,则$ab$的值是( )。

A.4
B.$-4$
C.16
D.$-16$

答案： 【解析】：已知$a + b = 3$，$a - b = 5$，将这两个方程相加可得：$(a + b) + (a - b) = 3 + 5$，即$2a = 8$，解得$a = 4$。把$a = 4$代入$a + b = 3$，可得$4 + b = 3$，解得$b = -1$。所以$ab = 4×(-1) = -4$。
【答案】：B

8. 某餐厅到超市购买某品牌均为$5kg$袋装的大米和面粉,大米每袋$a$元,面粉每袋$b$元,共买3袋大米,5袋面粉。则应支付( )元。

A.$3a + 5b$
B.$5a + 3b$
C.$3(a + b)$
D.$5(a + b)$

答案： 【解析】：
首先，我们需要计算大米的总费用。由于每袋大米的价格是$a$元，并且购买了3袋，所以大米的总费用是$3 × a = 3a$元。
接着，我们需要计算面粉的总费用。每袋面粉的价格是$b$元，并且购买了5袋，所以面粉的总费用是$5 × b = 5b$元。
最后，我们将大米和面粉的总费用相加，得到应支付的总金额，即$3a + 5b$元。
【答案】：A

9. 定义$\begin{vmatrix}a&b\\c&d\end{vmatrix} $为二阶行列式,规定它的运算法则为$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$,那么当$x = 1$时,二阶行列式$\begin{vmatrix}x + 1&1\\0&x - 1\end{vmatrix} $的值为( )。

A.1
B.2
C.0
D.$-1$

答案： 【解析】：根据二阶行列式的定义，有
$\begin{vmatrix}a&b\\c&d\end{vmatrix}= ad - bc$
将题目中给定的二阶行列式代入上述公式，得
$\begin{vmatrix}x + 1&1\\0&x - 1\end{vmatrix}= (x + 1)(x - 1) - 1 × 0$
化简得
$= x^2 - 1$
当 $x = 1$ 时，代入上述表达式，得
$= 1^2 - 1 = 0$
【答案】：C