《2025年暑假生活指导七年级山东教育出版社》

1. 计算：$3a\cdot2a^{2}= $______。$x^{5}÷ x^{3}= $______。

答案： 【解析】：对于第一个式子$3a\cdot2a^{2}$，根据单项式乘法法则，系数相乘，同底数幂相乘，系数$3×2 = 6$，同底数幂$a\cdot a^{2}=a^{1 + 2}=a^{3}$，所以结果为$6a^{3}$。
对于第二个式子$x^{5}÷x^{3}$，根据同底数幂除法法则，底数不变，指数相减，即$x^{5 - 3}=x^{2}$。
【答案】：$6a^{3}$；$x^{2}$

2. 小明模仿电视节目发明了一个魔术盒,当任意实数对$(a,b)$进入其中时,会得到一个新的实数：$a^{2}+b - 1$,例如把$(3,-2)$放入其中,就会得到$3^{2}+(-2)-1 = 6$。现将实数对$(-1,3)$放入其中,得到实数$m$,再将实数对$(m,1)$放入其中后,得到的实数是______。

答案： 【解析】：
1. 首先，根据题目中给出的魔术盒规则，当实数对$(a,b)$进入魔术盒时，会得到一个新的实数：$a^{2}+b - 1$。
2. 将实数对$(-1,3)$放入魔术盒，计算得到的实数为：
$m = (-1)^{2} + 3 - 1 = 1 + 3 - 1 = 3$
3. 接下来，将实数对$(m,1)$，即$(3,1)$放入魔术盒，计算得到的实数为：
$3^{2} + 1 - 1 = 9 + 1 - 1 = 9$
【答案】：9

3. 若$(mx^{3})\cdot(2x^{k})= -8x^{18}$,则适合此等式的$m= $______,$k= $______。

答案： 【解析】：根据单项式乘法法则，系数相乘，同底数幂相乘，底数不变指数相加。左边式子系数为$m×2 = 2m$，同底数幂部分为$x^{3 + k}$，所以左边结果为$2m x^{3 + k}$。已知等式右边为$-8x^{18}$，则可得方程组$\begin{cases}2m = -8\\3 + k = 18\end{cases}$，解第一个方程得$m = -4$，解第二个方程得$k = 15$。
【答案】：-4,15

4. 观察一列单项式：$x$,$3x^{2}$,$5x^{2}$,$7x$,$9x^{2}$,$11x^{2}$,…$$,则第2013个单项式是______。

答案： 【解析】：观察这列单项式，系数依次为1，3，5，7，9，11，…，是连续的奇数，第n个单项式的系数为2n-1。
再看字母及指数部分：x，x²，x²，x，x²，x²，…，可以发现每3个为一组，循环出现“x，x²，x²”。
计算2013除以3：2013÷3=671，没有余数，说明第2013个单项式是第671组的最后一个，对应的字母及指数为x²。
所以第2013个单项式的系数为2×2013 - 1 = 4025，字母及指数为x²，即第2013个单项式是4025x²。
【答案】：4025x²

5. 在$\triangle ABC$中,若$\angle A:\angle B:\angle C = 1:3:5$,这个三角形为______三角形。(按角的分类)

答案： 【解析】：
设$\angle A = x$，根据题意有：
$\angle A = x$
$\angle B = 3x$
$\angle C = 5x$
根据三角形的内角和性质，三角形的三个内角之和为$180^\circ$，所以：
$x + 3x + 5x = 180^\circ$
$9x = 180^\circ$
解得：
$x = 20^\circ$
代入得：
$\angle A = 20^\circ$
$\angle B = 60^\circ$
$\angle C = 100^\circ$
由于$\angle C = 100^\circ$，且$100^\circ ＞ 90^\circ$，所以这个三角形是钝角三角形。
【答案】：钝角

6. 已知$a$,$b满足a + b = 3$,$ab = 2$,则$a^{2}+b^{2}= $______。

答案： 【解析】：
已知 $a + b = 3$ 和 $ab = 2$，
我们需要求 $a^{2} + b^{2}$。
根据平方和公式，我们有：
$a^{2} + b^{2} = (a + b)^{2} - 2ab$
代入已知条件 $a + b = 3$ 和 $ab = 2$，我们得到：
$a^{2} + b^{2} = 3^{2} - 2 × 2 = 9 - 4 = 5$
【答案】：5

7. 在一个不透明的袋子中装有$n$个小球,这些球除颜色外均相同,其中红球有5个,如果从袋子中随机摸出一个球,这个球是红球的概率为$\frac{1}{3}$,那么$n$的值是______。

答案： 【解析】：已知袋子中红球有5个，从袋子中随机摸出一个球是红球的概率为$\frac{1}{3}$。根据概率公式，概率等于所求情况数与总情况数之比，即红球的个数除以球的总个数等于摸出红球的概率。设球的总个数为$n$，可列出方程$\frac{5}{n}=\frac{1}{3}$，解方程可得$n = 5×3 = 15$。
【答案】：15

8. 在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是______。

答案： 【解析】：在函数中，因变量是随着自变量的变化而变化的量。
在这个问题中，水温是随着所晒时间的长短而变化的，所以水温是因变量，所晒时间则是自变量。
【答案】：水温

9. 汽车开始行驶时,油箱中有油40升,如果每小时耗油5升,则油箱内余油量$y$(升)与行驶时间$x$(时)的关系式为______,该汽车最多可行驶______小时。

答案： 【解析】：
汽车开始行驶时，油箱中有油40升，这是初始油量。
每小时耗油5升，所以行驶x小时后，汽车会耗油5x升。
因此，油箱内余油量y（升）与行驶时间x（时）的关系式为：y = 40 - 5x。
为了找出汽车最多可行驶的时间，我们需要令y=0，并解出x的值。
即：40 - 5x = 0，
解这个方程，我们得到：x = 8。
所以，汽车最多可行驶8小时。
【答案】：
y = 40 - 5x；8。

10. 学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前进。如图所示,$l_{1}和l_{2}分别表示两人到小亮家的距离s(km)和时间t(h)$的关系,出发时小明在小亮前方______$km$,出发______$h$后两人相遇。

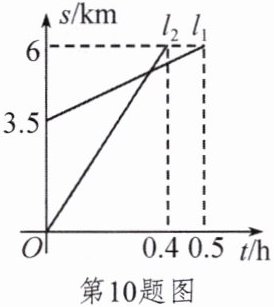
答案： 【解析】：由图像可知，当$t = 0$时，$l_{1}$对应的$s = 3.5km$，$l_{2}$对应的$s = 0km$，所以出发时小明在小亮前方$3.5km$。
两条直线$l_{1}$和$l_{2}$的交点表示两人相遇，交点对应的横坐标$t = 0.4h$，即出发$0.4h$后两人相遇。
【答案】：3.5；0.4

1. 将水匀速滴进如图所示的容器时,能正确反映容器中水的高度$(h)与时间(t)$之间对应关系的图象大致是( )。

答案： 【解析】：由图可知，容器下方较宽，上方较窄。当匀速滴水时，随着水位上升，容器的横截面积逐渐变小。根据体积公式$V = S × h$（$V$为体积，$S$为横截面积，$h$为高度），在体积变化率（即滴水量速度）一定的情况下，横截面积$S$越小，高度$h$的变化率越大，也就是水位上升得越来越快。因此，$h$与$t$的关系图象应该是一条斜率逐渐增大的曲线，选项B符合这一特征。
【答案】：B