8. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形。下列作法错误的是 (

B
)
答案:
B
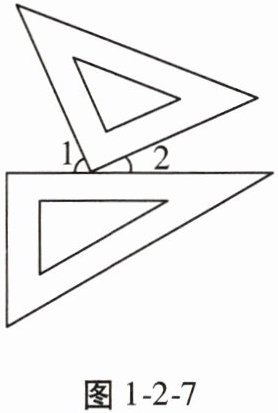
9. 一副三角尺按如图1-2-7所示的方式摆放,$\angle 2 = 25^{\circ}$,则$\angle 1=$
65
$^{\circ}$。
答案:
65
10. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射。由于折射率相同,所以在水中的平行光线,在空气中也是平行的。如图1-2-8,若$\angle 2-\angle 1 = 75^{\circ}$,则$\angle 3$与$\angle 4$的度数和是

$105^{\circ}$
。
答案:
$105^{\circ}$
11. 如图1-2-9,$AD// BC$,$AB// DC$,$\angle B = 60^{\circ}$,则$\angle D=$

$60^{\circ}$
。
答案:
$60^{\circ}$
12. 绚丽多彩的舞台离不开灯光的氛围,不同类型的灯呈现出不同的舞台灯光。光速灯发出的光速是一根明亮的细长的光柱,如图1-2-10,在舞台上方平行的灯轨$a$,$b$上分别安置了可以旋转的光速灯$A$和$C$,光速灯$A$的光束$AB$以每秒$6^{\circ}$的速度顺时针旋转$180^{\circ}$便立即回转,光速灯$C$的光束$CD$以每秒$2^{\circ}$的速度顺时针旋转$180^{\circ}$便立即停止。若光速灯$C$先旋转$6s$,光速灯$A$才开始旋转,当光速灯$A$旋转时间为______$s$时,两束光线平行。


答案:
3或43.5 解析:设光速灯A旋转时间为$t$ s,则光速灯C旋转的时间为$(t + 6)$ s,当AB旋转小于$180^{\circ}$时,如图所示。

因为$AB // CD$,
所以$∠1 = ∠2$ (两直线平行,同位角相等)。
因为$a // b$,
所以$∠2 = ∠3$ (两直线平行、内错角相等),
所以$∠1 = ∠3$。
因为AB以每秒$6^{\circ}$的速度顺时针旋转,CD以每秒$2^{\circ}$的速度顺时针旋转,
所以$∠1 = (6t)^{\circ}$, $∠3 = (12 + 2t)^{\circ}$,
所以$6t = 12 + 2t$,
所以$t = 3$。
当AB旋转大于$180^{\circ}$回转时,如图所示。

因为$AB // CD$, $a // b$,
所以$∠1 = ∠2$, $∠2 = ∠3$,
所以$∠1 = ∠3$。
因为$∠1 = [180 - (6t - 180)]^{\circ} = (360 - 6t)^{\circ}$, $∠3 = (12 + 2t)^{\circ}$,
所以$360 - 6t = 12 + 2t$,
所以$t = 43.5$。
综上,旋转时间为3 s或43.5 s。
3或43.5 解析:设光速灯A旋转时间为$t$ s,则光速灯C旋转的时间为$(t + 6)$ s,当AB旋转小于$180^{\circ}$时,如图所示。

因为$AB // CD$,
所以$∠1 = ∠2$ (两直线平行,同位角相等)。
因为$a // b$,
所以$∠2 = ∠3$ (两直线平行、内错角相等),
所以$∠1 = ∠3$。
因为AB以每秒$6^{\circ}$的速度顺时针旋转,CD以每秒$2^{\circ}$的速度顺时针旋转,
所以$∠1 = (6t)^{\circ}$, $∠3 = (12 + 2t)^{\circ}$,
所以$6t = 12 + 2t$,
所以$t = 3$。
当AB旋转大于$180^{\circ}$回转时,如图所示。

因为$AB // CD$, $a // b$,
所以$∠1 = ∠2$, $∠2 = ∠3$,
所以$∠1 = ∠3$。
因为$∠1 = [180 - (6t - 180)]^{\circ} = (360 - 6t)^{\circ}$, $∠3 = (12 + 2t)^{\circ}$,
所以$360 - 6t = 12 + 2t$,
所以$t = 43.5$。
综上,旋转时间为3 s或43.5 s。
13. 如图1-2-11①,“二八大杠”传统老式自行车承载了一代人的回忆,图②是它的几何示意图。已知$BC// DE$,$AB// CD$,当$\angle ABD = 70^{\circ}$,$\angle CBD = 44^{\circ}$时,$\angle CDE$的度数为

$66^{\circ}$
。
答案:
$66^{\circ}$
查看更多完整答案,请扫码查看


