《2025年暑假作业与生活陕西师范大学出版总社有限公司七年级数学北师大版》

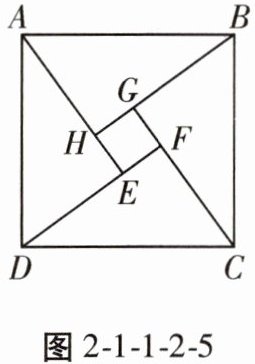
4. 如图2-1-1-2-5是“赵爽弦图”，$△ABH$、$△BCG$、$△CDF$和$△DAE$是四个全等的直角三角形，四边形ABCD和EFGH都是正方形。如果$AB = 10$，$EF = 2$，那么AH等于6。

答案： 6。解析：因为 $ AB = 10 $，$ EF = 2 $，
所以大正方形的面积是 100，小正方形的面积是 4，
所以四个直角三角形面积和为 $ 100 - 4 = 96 $，设 $ AE $ 为 $ a $，$ DE $ 为 $ b $，即 $ 4 \times \frac{1}{2}ab = 96 $，
所以 $ 2ab = 96 $，$ a^{2} + b^{2} = 100 $，
所以 $ (a + b)^{2} = a^{2} + b^{2} + 2ab = 100 + 96 = 196 $，
所以 $ a + b = 14 $。
因为 $ a - b = 2 $，
解得 $ a = 8 $，$ b = 6 $，
所以 $ AE = 8 $，$ AH = DE = 6 $，
所以 $ AH = 8 - 2 = 6 $。

5. 利用图2-1-1-2-6①或②两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理，这个定理称为勾股定理，该定理的数学表达式是$ a^{2} + b^{2} = c^{2} $。

答案： 勾股定理 $ a^{2} + b^{2} = c^{2} $

6. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图2-1-1-2-7所示）。如果大正方形的面积是13，小正方形的面积是1，直角三角形的两直角边分别为a，b，那么$(a + b)^{2}$的值是25。

答案： 25。解析：根据题意，结合勾股定理 $ a^{2} + b^{2} = 13 $①，
四个三角形的面积为 $ 4 \times \frac{1}{2}ab = 13 - 1 $，
所以 $ 2ab = 12 $②，
联立①②，得 $ (a + b)^{2} = 13 + 12 = 25 $。

例1 下面的每组数分别是一个三角形的三边长，分别以每组数为三边画出三角形，用量角器量一量，它们都是直角三角形吗？
①3，4，5；②5，12，13；③6，8，10。
答：图略。都是直角三角形。先判断最长边，再判断最长边的平方等于较小两边的平方和。

答案： 【解析】：对于①，最长边是5，$3^{2}+4^{2}=9 + 16 = 25 = 5^{2}$，满足最长边的平方等于较小两边的平方和，所以以3，4，5为三边的三角形是直角三角形；对于②，最长边是13，$5^{2}+12^{2}=25 + 144 = 169 = 13^{2}$，满足最长边的平方等于较小两边的平方和，所以以5，12，13为三边的三角形是直角三角形；对于③，最长边是10，$6^{2}+8^{2}=36 + 64 = 100 = 10^{2}$，满足最长边的平方等于较小两边的平方和，所以以6，8，10为三边的三角形是直角三角形。
【答案】：都是直角三角形