例2 一个零件的形状如图2-1-2-1所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量出了这个零件各边的尺寸,那么这个零件符合要求吗?
解:在△ABD中,已知AB=
解:在△ABD中,已知AB=
3
,AD=4
,BD=5
,计算AB²+AD²=3²+4²=9+16=25
,BD²=5²=25
,所以AB²+AD²=BD²,所以△ABD是直角三角形,∠A是直角。在△BCD中,已知DB=5
,BC=12
,CD=13
,计算DB²+BC²=5²+12²=25+144=169
,CD²=13²=169
,所以DB²+BC²=CD²,所以△BCD是直角三角形,∠DBC是直角。因此这个零件符合要求。
答案:
【解析】:在$\triangle ABD$中,已知$AB = 3$,$AD = 4$,$BD = 5$,根据勾股定理的逆定理,计算$AB^{2}+AD^{2}=3^{2}+4^{2}=9 + 16 = 25$,$BD^{2}=5^{2}=25$,所以$AB^{2}+AD^{2}=BD^{2}$,满足勾股定理逆定理,因此$\triangle ABD$是直角三角形,$\angle A$是直角。在$\triangle BCD$中,已知$DB = 5$,$BC = 12$,$CD = 13$,计算$DB^{2}+BC^{2}=5^{2}+12^{2}=25 + 144 = 169$,$CD^{2}=13^{2}=169$,所以$DB^{2}+BC^{2}=CD^{2}$,满足勾股定理逆定理,因此$\triangle BCD$是直角三角形,$\angle DBC$是直角。
【答案】:这个零件符合要求。
【答案】:这个零件符合要求。
1. 下列各组数中,能作为直角三角形的三边长的是(
A. 1.5,2,3
B. 2,3,4
C. $1,\frac{4}{3},\frac{5}{3}$
D. 5,13,14
C
)A. 1.5,2,3
B. 2,3,4
C. $1,\frac{4}{3},\frac{5}{3}$
D. 5,13,14
答案:
C
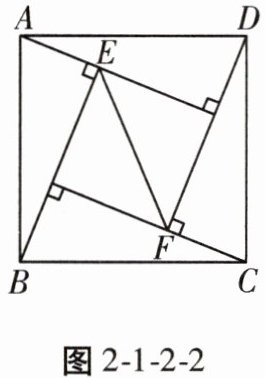
2. 如图2-1-2-2是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=5,BE=12,则$EF^{2}$的值是(
A. 98
B. 144
C. 25
D. 49
A
)
A. 98
B. 144
C. 25
D. 49
答案:
A
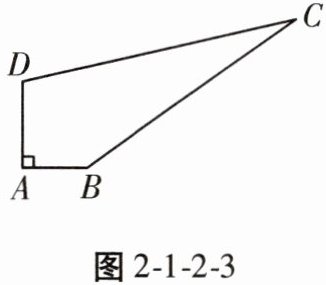
3. 如图2-1-2-3,李伯伯家有一块四边形田地,其中∠A=90°,AB=3m,BC=12m,CD=13m,AD=4m,则这块地的面积为(
A. $36m^{2}$
B. $42m^{2}$
C. $66m^{2}$
D. $72m^{2}$
A
)
A. $36m^{2}$
B. $42m^{2}$
C. $66m^{2}$
D. $72m^{2}$
答案:
A
4. 在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地。送行二步与人齐,五尺人高曾记。仕女佳人争蹴,终朝笑语欢嬉。良工高士素好奇,算出索长有几。”此问题可理解为:如图2-1-2-4,有一架秋千,当它静止时,踏板离地距离AB的长度为1尺。将它往前水平推送10尺,即$A'C=10$尺,则此时秋千的踏板离地距离$A'D$就和身高5尺的人一样高。若运动过程中秋千的绳索始终拉得很直,则绳索OA长为______尺。(注:尺是我国传统长度单位,1尺≈0.33m)


14.5
答案:
14.5 解析:设秋千的绳索 OA 长为 x 尺。
由题意知:$OC = x - (5 - 1) = (x - 4)$尺,
$CA' = 10$尺,$OA' = x$尺,
在$Rt\triangle OCA'$中,$OC^{2} + CA'^{2} = OA'^{2}$,
所以$(x - 4)^{2} + 10^{2} = x^{2}$,
解得$x = 14.5$。
由题意知:$OC = x - (5 - 1) = (x - 4)$尺,
$CA' = 10$尺,$OA' = x$尺,
在$Rt\triangle OCA'$中,$OC^{2} + CA'^{2} = OA'^{2}$,
所以$(x - 4)^{2} + 10^{2} = x^{2}$,
解得$x = 14.5$。
查看更多完整答案,请扫码查看


