《2025年暑假作业与生活陕西师范大学出版总社有限公司七年级数学北师大版》

1. 相交线
(1) 两条直线相交，有公共顶点且两边互为反向延长线的两个角是对顶角，其性质是对顶角相等。
(2) 两条直线相交成四个角，如果有一个角是直角，那么称这两条直线互相垂直，其中一条直线叫作另一条直线的垂线，它们的交点叫作垂足。
(3) 同一平面内，过一点有且只有一条直线与已知直线垂直。
(4) 直线外一点到这条直线的垂线段的长度，叫作点到直线的距离。

答案：
(1)对顶角　对顶角相等
(2)互相垂直　垂线　垂足
(3)有且只有
(4)垂线段

2. 平行线
(1) 在同一平面内，不相交的两条直线叫作平行线。
(2) 平行线的判定方法：
同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行。过直线外一点有且只有一条直线与这条直线平行。平行于同一条直线的两条直线互相平行。

答案：
(1)不相交
(2)相等　相等　互补　有且只有　互相平行

3. 平行线的性质
两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补。

答案： 相等　相等　互补

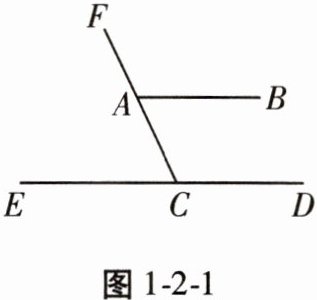
1. 如图1-2-1，已知$AB// ED$，$\angle ECF = 65^{\circ}$，则$\angle BAC$的度数为 (B)

A. $115^{\circ}$
B. $65^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$

答案： B