16. 若$a^{m}=a^{n}$($a>0$且$a\neq 1$,$m$,$n$是正整数),则$m = n$。你能利用上面的结论解决下面两个问题吗?
(1)已知$2× 8^{x}× 16=2^{23}$,求$x$的值;
解: $2 × 8^x × 16 = 2^{23}$,
$2 × (2^3)^x × 2^4 = 2^{23}$,
$2 × 2^{3x} × 2^4 = 2^{23}$,
$2^{3x + 5} = 2^{23}$,
$3x + 5 = 23$,
解得 $x =$
(2)已知$2^{x + 3}× 3^{x + 3}=36^{x - 2}$,求$x$的值。
解: $2^{x + 3} × 3^{x + 3} = 36^{x - 2}$,
$6^{x + 3} = (6^2)^{x - 2}$,
$6^{x + 3} = 6^{2x - 4}$,
$x + 3 = 2x - 4$,
解得 $x =$
(1)已知$2× 8^{x}× 16=2^{23}$,求$x$的值;
解: $2 × 8^x × 16 = 2^{23}$,
$2 × (2^3)^x × 2^4 = 2^{23}$,
$2 × 2^{3x} × 2^4 = 2^{23}$,
$2^{3x + 5} = 2^{23}$,
$3x + 5 = 23$,
解得 $x =$
6
。(2)已知$2^{x + 3}× 3^{x + 3}=36^{x - 2}$,求$x$的值。
解: $2^{x + 3} × 3^{x + 3} = 36^{x - 2}$,
$6^{x + 3} = (6^2)^{x - 2}$,
$6^{x + 3} = 6^{2x - 4}$,
$x + 3 = 2x - 4$,
解得 $x =$
7
。
答案:
解:
(1) $2 \times 8^x \times 16 = 2^{23}$,
$2 \times (2^3)^x \times 2^4 = 2^{23}$,
$2 \times 2^{3x} \times 2^4 = 2^{23}$,
$2^{3x + 5} = 2^{23}$,
$3x + 5 = 23$,
解得 $x = 6$。
(2) $2^{x + 3} \times 3^{x + 3} = 36^{x - 2}$,
$6^{x + 3} = (6^2)^{x - 2}$,
$6^{x + 3} = 6^{2x - 4}$,
$x + 3 = 2x - 4$,
解得 $x = 7$。
(1) $2 \times 8^x \times 16 = 2^{23}$,
$2 \times (2^3)^x \times 2^4 = 2^{23}$,
$2 \times 2^{3x} \times 2^4 = 2^{23}$,
$2^{3x + 5} = 2^{23}$,
$3x + 5 = 23$,
解得 $x = 6$。
(2) $2^{x + 3} \times 3^{x + 3} = 36^{x - 2}$,
$6^{x + 3} = (6^2)^{x - 2}$,
$6^{x + 3} = 6^{2x - 4}$,
$x + 3 = 2x - 4$,
解得 $x = 7$。
17. 数形结合思想是初中数学学习中一种很重要的思维方法,“数”的精确描述与“形”的直观刻画,使代数问题与几何问题相互转化。“以形释数”是利用数形结合思想解决代数问题的一种体现,做整式的乘法运算时,利用几何直观的面积法获取结论,在整式运算中时常运用。
【问题探究】
探究:如图1-1-2①是一个长为$2m$、宽为$2n$的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形。
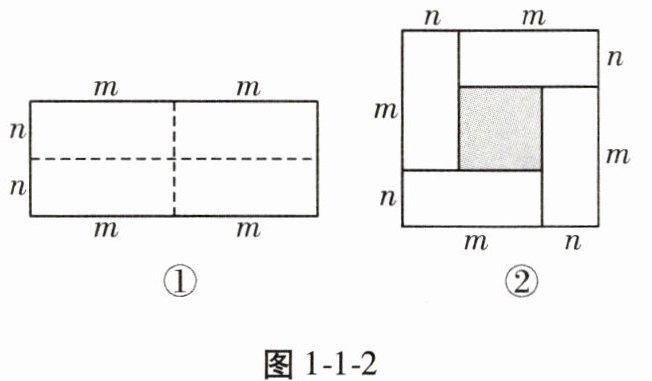
请用两种不同的方法表示图1-1-2②中阴影部分的面积。
方法1:
方法2:
【得出结论】
观察如图1-1-2②,请你写出下列三个代数式:$(m + n)^{2}$,$(m - n)^{2}$,$mn$之间的等量关系。
【应用结论】
根据以上等量关系,解决如下问题:已知:$a - b = 5$,$ab = -6$,求$(a + b)^{2}$的值。
【问题探究】
探究:如图1-1-2①是一个长为$2m$、宽为$2n$的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形。

请用两种不同的方法表示图1-1-2②中阴影部分的面积。
方法1:
$(m + n)^2 - 4mn$
;方法2:
$(m - n)^2$
。【得出结论】
观察如图1-1-2②,请你写出下列三个代数式:$(m + n)^{2}$,$(m - n)^{2}$,$mn$之间的等量关系。
【应用结论】
根据以上等量关系,解决如下问题:已知:$a - b = 5$,$ab = -6$,求$(a + b)^{2}$的值。
答案:
解: 【问题探究】
方法 1: $S_{阴影} = (m + n)^2 - 4mn$。
方法 2: $S_{阴影} = (m - n)^2$。
【得出结论】根据题意可知, $(m + n)^2 - 4mn = (m - n)^2$。
【应用结论】根据题意可知, $a - b = 5$, $ab = -6$,
$(a + b)^2 = (a - b)^2 + 4ab = 5^2 + 4 \times (-6) = 25 - 24 = 1$。
方法 1: $S_{阴影} = (m + n)^2 - 4mn$。
方法 2: $S_{阴影} = (m - n)^2$。
【得出结论】根据题意可知, $(m + n)^2 - 4mn = (m - n)^2$。
【应用结论】根据题意可知, $a - b = 5$, $ab = -6$,
$(a + b)^2 = (a - b)^2 + 4ab = 5^2 + 4 \times (-6) = 25 - 24 = 1$。
查看更多完整答案,请扫码查看


