1. 图2-1-1-2-3是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是 (
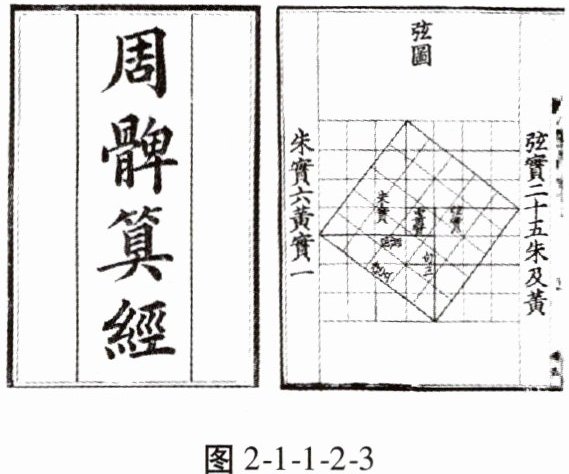
A. 黄金分割
B. 垂径定理
C. 勾股定理
D. 正弦定理
C
)
A. 黄金分割
B. 垂径定理
C. 勾股定理
D. 正弦定理
答案:
C
2. 勾股定理是“人类最伟大的十个科学发现之一”。我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”。2002年在北京召开的国际数学大会选它作为会徽。下列图案中是“赵爽弦图”的是 (
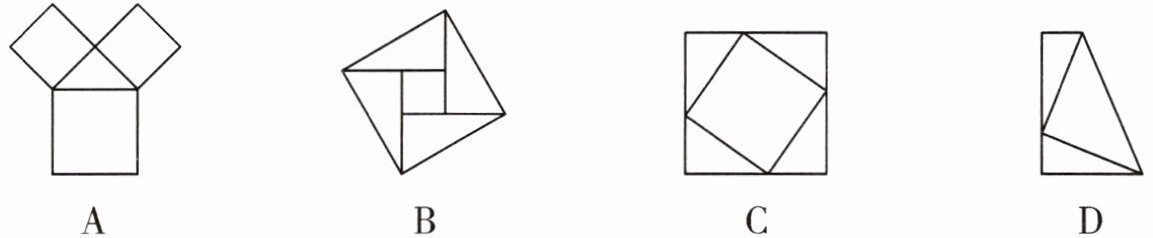
B
)
答案:
B
3. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲。如图2-1-1-2-4所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形。设直角三角形较长直角边长为a,较短直角边长为b。若$ab = 8$,大正方形的面积为25,则小正方形的边长为 (
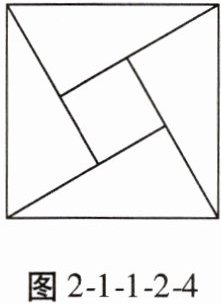
A. 9
B. 6
C. 4
D. 3
D
)
A. 9
B. 6
C. 4
D. 3
答案:
D
查看更多完整答案,请扫码查看


