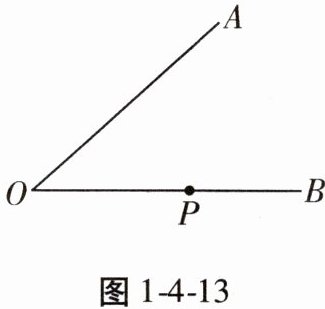
16. 如图1-4-13,P为$∠AOB$的边OB上的一点,请用尺规作图法,过点P作$∠CPB$,使得$∠CPB=∠AOB$,且点C在$∠AOB$内。(保留作图痕迹,不写作法)

答案:
解:如图,$ \angle CPB$ 即为所求作。

解:如图,$ \angle CPB$ 即为所求作。

17. 小明利用一根3m长的竿子来测量路灯的高度。他的方法是这样的:如图1-4-14,在路灯前选一点P,使$BP=3m$,并测得$∠APB=70^{\circ}$,然后把竖直的竿子CD($CD=3m$)在BP的延长线上移动,使$∠DPC=20^{\circ}$,此时量得$BD=11.2m$。根据这些数据,小明计算出了路灯的高度。你知道小明计算出的路灯的高度是多少?为什么?

路灯的高度是
理由:因为 $ \angle CPD = 20^{\circ}$,$ \angle APB = 70^{\circ}$,$ \angle CDP = \angle ABP = 90^{\circ}$,所以 $ \angle DCP = \angle APB = 70^{\circ}$。在 $ \triangle CPD$ 和 $ \triangle PAB$ 中,$\left\{ \begin{array}{l} \angle CDP = \angle PBA, \\ DC = PB, \\ \angle DCP = \angle BPA, \end{array} \right. $所以 $ \triangle CPD \cong \triangle PAB(ASA)$,所以 $DP = AB$。因为 $DB = 11.2 \, \text{m}$,$PB = 3 \, \text{m}$,所以 $DP = 11.2 - 3 = 8.2(\text{m})$。所以 $AB = 8.2 \, \text{m}$。

路灯的高度是
8.2m
。理由:因为 $ \angle CPD = 20^{\circ}$,$ \angle APB = 70^{\circ}$,$ \angle CDP = \angle ABP = 90^{\circ}$,所以 $ \angle DCP = \angle APB = 70^{\circ}$。在 $ \triangle CPD$ 和 $ \triangle PAB$ 中,$\left\{ \begin{array}{l} \angle CDP = \angle PBA, \\ DC = PB, \\ \angle DCP = \angle BPA, \end{array} \right. $所以 $ \triangle CPD \cong \triangle PAB(ASA)$,所以 $DP = AB$。因为 $DB = 11.2 \, \text{m}$,$PB = 3 \, \text{m}$,所以 $DP = 11.2 - 3 = 8.2(\text{m})$。所以 $AB = 8.2 \, \text{m}$。
答案:
解:因为 $ \angle CPD = 20^{\circ}$,$ \angle APB = 70^{\circ}$,$ \angle CDP = \angle ABP = 90^{\circ}$,
所以 $ \angle DCP = \angle APB = 70^{\circ}$。
在 $ \triangle CPD$ 和 $ \triangle PAB$ 中,
$\left\{ \begin{array}{l} \angle CDP = \angle PBA, \\ DC = PB, \\ \angle DCP = \angle BPA, \end{array} \right. $
所以 $ \triangle CPD \cong \triangle PAB(ASA)$,
所以 $DP = AB$。
因为 $DB = 11.2 \, \text{m}$,$PB = 3 \, \text{m}$,
所以 $DP = 11.2 - 3 = 8.2(\text{m})$。
所以 $AB = 8.2 \, \text{m}$。
答:路灯的高度 $AB$ 是 $8.2 \, \text{m}$。
所以 $ \angle DCP = \angle APB = 70^{\circ}$。
在 $ \triangle CPD$ 和 $ \triangle PAB$ 中,
$\left\{ \begin{array}{l} \angle CDP = \angle PBA, \\ DC = PB, \\ \angle DCP = \angle BPA, \end{array} \right. $
所以 $ \triangle CPD \cong \triangle PAB(ASA)$,
所以 $DP = AB$。
因为 $DB = 11.2 \, \text{m}$,$PB = 3 \, \text{m}$,
所以 $DP = 11.2 - 3 = 8.2(\text{m})$。
所以 $AB = 8.2 \, \text{m}$。
答:路灯的高度 $AB$ 是 $8.2 \, \text{m}$。
1. (2024·陕西中考)如图1-4-15,在$\triangle ABC$中,$∠BAC=90^{\circ}$,AD是BC边上的高,E是BC的中点,连接AE,则图中的直角三角形共有 (

A. 2个
B. 3个
C. 4个
D. 5个
C
)
A. 2个
B. 3个
C. 4个
D. 5个
答案:
C
2. (2024·长沙中考)如图1-4-16,在$\triangle ABC$中,$∠BAC=60^{\circ}$,$∠B=50^{\circ}$,$AD// BC$,则$∠1$的度数为 (

A. $50^{\circ}$
B. $60^{\circ}$
C. $70^{\circ}$
D. $80^{\circ}$
C
)
A. $50^{\circ}$
B. $60^{\circ}$
C. $70^{\circ}$
D. $80^{\circ}$
答案:
C
3. (2024·牡丹江中考)如图1-4-17,在$\triangle ABC$中,D是AB上一点,$CF// AB$,D,E,F三点共线,请添加一个条件____
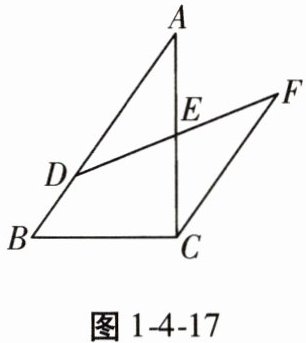
$AD = CF$
,使得$AE=CE$。(只添一种情况即可)
答案:
$AD = CF$(答案不唯一)
查看更多完整答案,请扫码查看


