《2025年暑假作业长江少年儿童出版社五年级数学》

4 为了做好环境消毒工作,环卫处购买了一辆小型喷雾式汽车。已知汽车药液箱从里面量长 2 m,宽 1 m,高 0.6 m,如果它每分钟喷出药液 4.8 L,那么它喷完一箱药液需要用多少分钟?

答案： 本题主要考查长方体的体积公式。
解析：
题目考查的是长方体的体积公式，即体积 = 长 × 宽 × 高，同时还需要进行单位换算，因为题目中给出的喷出药液的速度单位是升/分钟，而药液箱的尺寸单位是米，所以需要将体积从立方米换算为升。
首先，我们需要计算药液箱的体积。
药液箱的体积 = 长 × 宽 × 高 = 2 × 1 × 0.6 = 1.2（立方米）。
因为1立方米 = 1000升，所以药液箱的体积也可以表示为：
1.2立方米 = 1200升。
接下来，我们用药液箱的总体积除以每分钟喷出的药液量，就可以得到喷完一箱药液所需的时间：
所需时间 = 药液箱体积 ÷ 每分钟喷出药液量 = 1200 ÷ 4.8 = 250（分钟）。
答案：
它喷完一箱药液需要用250分钟。

5 一盒棋子,4 枚 4 枚地数多 3 枚,5 枚 5 枚地数多 4 枚,6 枚 6 枚地数少 1 枚,这盒棋子的枚数在 150 ~ 200 之间。问:这盒棋子共有多少枚?

答案： 解析：
题目考查最小公倍数的应用以及逻辑推理能力。
首先，根据题目条件，知道棋子数量在150~200之间。
接下来，根据题目给出的数棋子的条件来找出符合的数：
4枚4枚地数多3枚，可以理解为如果再加1枚，就可以被4整除。
5枚5枚地数多4枚，同样可以理解为如果再加1枚，就可以被5整除。
6枚6枚地数少1枚，这个条件说明如果棋子数量再加1枚，就可以被6整除。
综合以上三个条件，可以得出：棋子的数量加1枚后，应该是4、5、6的公倍数。
为了找到4、5、6的最小公倍数，可以先分解它们的质因数：
4 = 2 × 2，
5 = 5，
6 = 2 × 3，
所以，4、5、6的最小公倍数是 2 × 2 × 3 × 5 = 60，
但是，因为棋子数量在150~200之间，所以需要找到这个范围内的一个数，这个数加1后是60的倍数。
可以尝试60的倍数：60, 120, 180, ... ，发现在150~200之间的是180-1=179（加1前），180+1=181（超出范围），
而179+1=180，正好是60的3倍，符合条件。
同时，179除以4余3，除以5余4，除以6少1，也符合题目给出的数棋子的条件。
答案：
这盒棋子共有179枚。

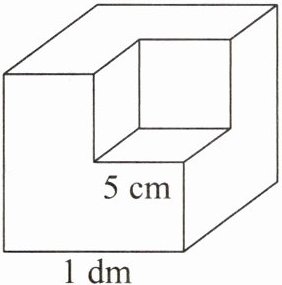
在一个棱长为 1 dm 的正方体木块的一角挖去一个棱长为 5 cm 的小正方体木块(如下图)。剩下部分的体积是多少立方厘米? 表面积是多少平方分米?
9

答案： 解析：本题考查正方体体积和表面积的计算以及对图形变化后体积和表面积变化情况的理解。
大正方体棱长为$1dm$，因为$1dm = 10cm$，根据正方体体积公式$V=a^3$（$V$为体积，$a$为棱长），可得大正方体体积$V_1 = 10×10×10 = 1000$（$cm^3$）。
小正方体棱长为$5cm$，同理可得小正方体体积$V_2 = 5×5×5 = 125$（$cm^3$）。
剩下部分的体积等于大正方体体积减去小正方体体积，即$V = V_1 - V_2 = 1000 - 125 = 875$（$cm^3$）。
原大正方体一个面的面积为$1×1 = 1$（$dm^2$），大正方体表面积为$6×1 = 6$（$dm^2$）。
在一角挖去小正方体后，原来大正方体的表面积并没有发生变化，因为挖去小正方体后，减少了小正方体的$3$个面，但同时又露出了与这$3$个面相同的$3$个面，所以剩下部分的表面积仍然是$6dm^2$。
答案：剩下部分的体积是$875cm^3$，表面积是$6dm^2$。