《2025年暑假作业长江少年儿童出版社五年级数学》

4 学校开运动会,五(1)班有45名同学参加,其中$\frac {1}{3}$的同学参加跳绳项目,$\frac {1}{5}$的同学参加跑步项目,5名同学参加跳高项目,其余的当啦啦队。根据上面的信息,请你提出一个数学问题并解答。

答案： 解析：
本题考查分数乘法的意义和实际应用以及提出问题的能力。
首先，根据题目信息，可以提出一个数学问题：当啦啦队的同学有多少人？
为了解答这个问题，需要先计算参加跳绳和跑步项目的同学人数，然后用总人数减去这些人数和参加跳高项目的人数，就可以得到啦啦队的人数。
根据分数乘法的意义，参加跳绳项目的同学人数为：
$45 × \frac{1}{3} = 15(人)$，
参加跑步项目的同学人数为：
$45 × \frac{1}{5} = 9(人)$，
已知参加跳高项目的同学有5人，所以，当啦啦队的同学人数为：
$45 - 15 - 9 - 5 = 16(人)$，
答案：
问题：当啦啦队的同学有多少人？
解答：当啦啦队的同学有16人。

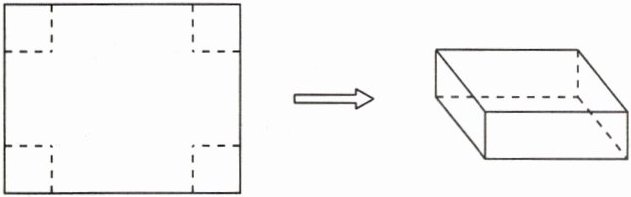
5 一张长25cm、宽20cm的长方形铁皮,从它的四个角各剪去一个边长为5cm的正方形,然后将剩余部分焊接成一个无盖的长方体铁盒。这个无盖的长方体铁盒的表面积是多少平方厘米?它的容积是多少毫升?(损耗忽略不计)

答案： 解析：本题主要考查长方体的表面积和容积的计算。需要先根据题意求出焊接后的无盖长方体铁盒的长、宽、高，再分别计算其表面积和容积。
计算无盖长方体铁盒的长、宽、高：
已知长方形铁皮长$25cm$、宽$20cm$，从它的四个角各剪去一个边长为$5cm$的正方形。
那么焊接成的无盖长方体铁盒的长为：$25 - 5× 2= 25 - 10 = 15$（$cm$）；
宽为：$20 - 5× 2 = 20 - 10 = 10$（$cm$）；
高就是剪去的正方形的边长，即$5cm$。
计算无盖长方体铁盒的表面积：
长方体表面积公式为$S=(ab + ah + bh)× 2$（$a$为长，$b$为宽，$h$为高），由于该铁盒无盖，所以表面积为$S = ab+(ah + bh)× 2$。
把$a = 15cm$，$b = 10cm$，$h = 5cm$代入可得：
$15× 10+(15× 5 + 10× 5)× 2$
$= 150+(75 + 50)× 2$
$= 150 + 125× 2$
$= 150 + 250$
$= 400$（$cm^{2}$）
也可以这样计算：原来长方形铁皮的面积为$25× 20 = 500cm^{2}$，剪去的四个正方形的面积为$5× 5× 4 = 100cm^{2}$，则无盖长方体铁盒的表面积为$500 - 100 = 400cm^{2}$。
计算无盖长方体铁盒的容积：
长方体容积公式为$V = abh$，把$a = 15cm$，$b = 10cm$，$h = 5cm$代入可得：
$V = 15× 10× 5 = 750$（$cm^{3}$）
因为$1cm^{3}=1ml$，所以$750cm^{3}=750ml$。
答案：表面积是$400$平方厘米，容积是$750$毫升。

学校实验室里有1g、2g、4g和8g的砝码各一个,在搬迁的过程中丢失了一个砝码,导致无法用它们直接称出12g和7g的物体的质量,丢失的砝码是(4)g的。

答案： 解析：
首先，我们考虑如何使用这些砝码来称出12g和7g的质量。
对于12g，我们可以使用8g+4g=12g的组合。
对于7g，我们可以使用4g+2g+1g=7g的组合。
但是，题目中说无法直接称出12g和7g的质量，这意味着至少有一个砝码是丢失的，导致上述组合无法实现。
我们观察上述两个组合，发现只有4g的砝码在两个组合中都出现了。
如果我们丢失了4g的砝码，那么：
对于12g，我们无法使用8g+4g的组合，因为4g的砝码已经丢失。
对于7g，我们也无法使用4g+2g+1g的组合，同样因为4g的砝码丢失。
因此，丢失的砝码只能是4g的。
答案：
丢失的砝码是4g的。