《2025年暑假作业长江少年儿童出版社五年级数学》

3 某工厂有男职工48人,女职工72人。男、女职工各占全厂职工总人数的几分之几？

答案： 解析：本题考查比例的计算。需要先求出总人数，再分别计算男女职工所占的比例。
全厂职工总人数：
$48 + 72 = 120$（人）。
男职工占全厂职工总人数的比例：
$\frac{48}{120} = \frac{2}{5}$。
女职工占全厂职工总人数的比例：
$\frac{72}{120} = \frac{3}{5}$。
答案：男职工占全厂职工总人数的$\frac{2}{5}$，女职工占全厂职工总人数的$\frac{3}{5}$。

4 武汉某早餐店刚出锅了一大块长方形豆皮,长63cm,宽45cm,在不浪费的情况下,将它分成大小相等且尽可能大的正方形豆皮。此时正方形小豆皮的边长是多少？一共可以切成多少块？

答案： 要将长63cm、宽45cm的长方形豆皮分成大小相等且尽可能大的正方形且不浪费，正方形的边长应为63和45的最大公因数。
解：
63的因数：1, 3, 7, 9, 21, 63
45的因数：1, 3, 5, 9, 15, 45
63和45的最大公因数是9，即正方形边长为9cm。
长可分：63÷9=7（块）
宽可分：45÷9=5（块）
总块数：7×5=35（块）
答：正方形小豆皮的边长是9cm，一共可以切成35块。

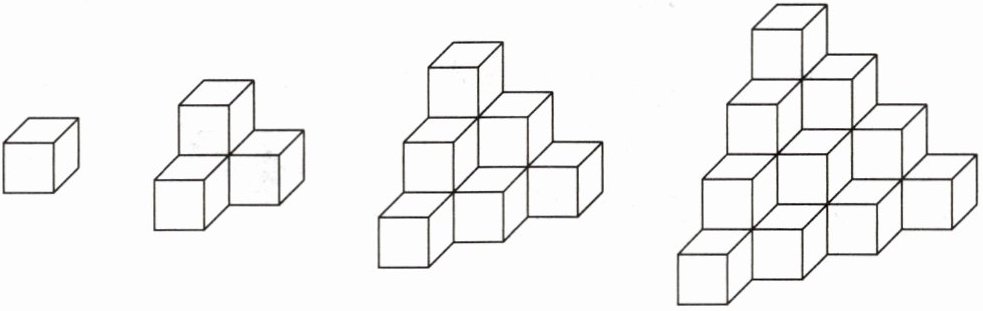
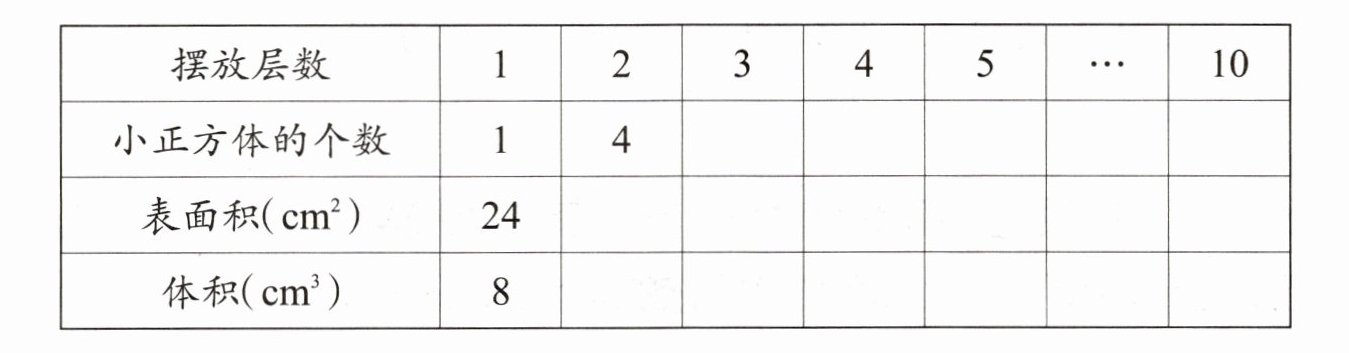
把一些棱长为2cm的小正方体摆成下面的形状,然后完成下表。

答案：
解析：
本题考查了正方体的表面积和体积的计算及应用。
根据图形可知，摆放层数为$1$时，小正方体的个数是$1$个；
摆放层数为$2$时，小正方体的个数是$1+3=4$（个）；
摆放层数为$3$时，小正方体的个数是$1+3+5=9$（个）；
摆放层数为$4$时，小正方体的个数是$1+3+5+7=16$（个）；
摆放层数为$5$时，小正方体的个数是$1+3+5+7+9=25$（个）；
$\cdots$
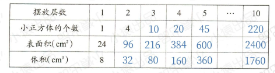
摆放层数为$10$时，小正方体的个数是$1+3+5+7+9+11+13+15+17+19=100$（个）。
正方体的表面积：$棱长×棱长×6$
正方体的体积：$棱长×棱长×棱长$
根据图形可知，摆放层数为$1$时，表面积是$2×2×6=24$（$cm^2$）；
摆放层数为$2$时，表面积是$2×2×18=72$（$cm^2$）；
摆放层数为$3$时，表面积是$2×2×36=144$（$cm^2$）；
摆放层数为$4$时，表面积是$2×2×60=240$（$cm^2$）；
摆放层数为$5$时，表面积是$2×2×90=360$（$cm^2$）；
$\cdots$
摆放层数为$10$时，表面积是$2×2×600=2400$（$cm^2$）。
根据图形可知，摆放层数为$1$时，体积是$2×2×2=8$（$cm^3$）；
摆放层数为$2$时，体积是$2×2×2×4=32$（$cm^3$）；
摆放层数为$3$时，体积是$2×2×2×9=72$（$cm^3$）；
摆放层数为$4$时，体积是$2×2×2×16=128$（$cm^3$）；
摆放层数为$5$时，体积是$2×2×2×25=200$（$cm^3$）；
$\cdots$
摆放层数为$10$时，体积是$2×2×2×100=800$（$cm^3$）。
答案：