1 直接写出得数。
$\frac { 3 } { 8 } + \frac { 1 } { 8 } = $
$\frac { 1 } { 3 } + \frac { 1 } { 2 } = $
$\frac { 3 } { 4 } - \frac { 1 } { 2 } = $
$3 ^ { 3 } = $
$\frac { 3 } { 8 } + \frac { 1 } { 8 } = $
$\frac{1}{2}$
$\frac { 5 } { 9 } - \frac { 2 } { 9 } = $$\frac{1}{3}$
$\frac { 5 } { 6 } - \frac { 5 } { 6 } = $0
$\frac { 1 } { 3 } + \frac { 1 } { 2 } = $
$\frac{5}{6}$
$1 - \frac { 5 } { 8 } = $$\frac{3}{8}$
$\frac { 7 } { 10 } + \frac { 5 } { 10 } = $$\frac{6}{5}$
$\frac { 3 } { 4 } - \frac { 1 } { 2 } = $
$\frac{1}{4}$
$\frac { 3 } { 4 } - \frac { 3 } { 4 } = $0
$\frac { 5 } { 11 } + \frac { 4 } { 11 } = $$\frac{9}{11}$
$3 ^ { 3 } = $
27
$5 ^ { 3 } = $125
$4 ^ { 3 } - 3 ^ { 2 } = $55
答案:
解析:
这些题目主要考察分数的加减运算,整数的乘方运算。
对于分数的加减,需要找到通分母,然后进行分子的加减。
对于整数的乘方,直接计算即可。
答案:
$\frac{3}{8} + \frac{1}{8} = \frac{4}{8} = \frac{1}{2}$;
$\frac{5}{9} - \frac{2}{9} = \frac{3}{9} = \frac{1}{3}$;
$\frac{5}{6} - \frac{5}{6} = 0$;
$\frac{1}{3} + \frac{1}{2} = \frac{2}{6} + \frac{3}{6} = \frac{5}{6}$;
$1 - \frac{5}{8} = \frac{8}{8} - \frac{5}{8} = \frac{3}{8}$;
$\frac{7}{10} + \frac{5}{10} = \frac{12}{10} = \frac{6}{5}$;
$\frac{3}{4} - \frac{1}{2} = \frac{3}{4} - \frac{2}{4} = \frac{1}{4}$;
$\frac{3}{4} - \frac{3}{4} = 0$;
$\frac{5}{11} + \frac{4}{11} = \frac{9}{11}$;
$3^3 = 27$;
$5^3 = 125$;
$4^3 - 3^2 = 64 - 9 = 55$。
这些题目主要考察分数的加减运算,整数的乘方运算。
对于分数的加减,需要找到通分母,然后进行分子的加减。
对于整数的乘方,直接计算即可。
答案:
$\frac{3}{8} + \frac{1}{8} = \frac{4}{8} = \frac{1}{2}$;
$\frac{5}{9} - \frac{2}{9} = \frac{3}{9} = \frac{1}{3}$;
$\frac{5}{6} - \frac{5}{6} = 0$;
$\frac{1}{3} + \frac{1}{2} = \frac{2}{6} + \frac{3}{6} = \frac{5}{6}$;
$1 - \frac{5}{8} = \frac{8}{8} - \frac{5}{8} = \frac{3}{8}$;
$\frac{7}{10} + \frac{5}{10} = \frac{12}{10} = \frac{6}{5}$;
$\frac{3}{4} - \frac{1}{2} = \frac{3}{4} - \frac{2}{4} = \frac{1}{4}$;
$\frac{3}{4} - \frac{3}{4} = 0$;
$\frac{5}{11} + \frac{4}{11} = \frac{9}{11}$;
$3^3 = 27$;
$5^3 = 125$;
$4^3 - 3^2 = 64 - 9 = 55$。
2 判断题。(对的画“√”,错的画“×”)
(1)一个分数,不是真分数就是假分数。 (
(2)将 20g 糖放入到 100g 水中,这时糖占糖水的 $$ \frac { 1 } { 5 } $$ 。 (
(3)大于 0 的带分数也一定大于 1。 (
(4)分数的分子越大,它的分数单位就越小。 (
(5)两个数的最小公倍数一定比这两个数都大。 (
(1)一个分数,不是真分数就是假分数。 (
×
)(2)将 20g 糖放入到 100g 水中,这时糖占糖水的 $$ \frac { 1 } { 5 } $$ 。 (
×
)(3)大于 0 的带分数也一定大于 1。 (
√
)(4)分数的分子越大,它的分数单位就越小。 (
×
)(5)两个数的最小公倍数一定比这两个数都大。 (
×
)
答案:
解析:
(1) 分数可以分为真分数、假分数和带分数。真分数是分子小于分母的分数,假分数是分子大于或等于分母的分数。由于题目没有提到带分数,所以此题的说法是不准确的。
答案:×
(2) 糖占糖水的比例应该是糖的质量除以糖和水的总质量。所以比例应该是 $ \frac{20}{20+100} = \frac{20}{120} = \frac{1}{6} $,与题目中的 $ \frac{1}{5} $ 不符。
答案:×
(3) 带分数由整数部分和真分数部分组成,由于整数部分至少为1,所以带分数一定大于1。
答案:√
(4) 分数的分数单位是由分母决定的,与分子大小无关。例如,$ \frac{2}{3} $ 和 $ \frac{1}{3} $ 的分数单位都是 $ \frac{1}{3} $。
答案:×
(5) 两个数的最小公倍数可能等于这两个数中的较大者,例如2和4的最小公倍数是4,并不比两个数都大。
答案:×
(1) 分数可以分为真分数、假分数和带分数。真分数是分子小于分母的分数,假分数是分子大于或等于分母的分数。由于题目没有提到带分数,所以此题的说法是不准确的。
答案:×
(2) 糖占糖水的比例应该是糖的质量除以糖和水的总质量。所以比例应该是 $ \frac{20}{20+100} = \frac{20}{120} = \frac{1}{6} $,与题目中的 $ \frac{1}{5} $ 不符。
答案:×
(3) 带分数由整数部分和真分数部分组成,由于整数部分至少为1,所以带分数一定大于1。
答案:√
(4) 分数的分数单位是由分母决定的,与分子大小无关。例如,$ \frac{2}{3} $ 和 $ \frac{1}{3} $ 的分数单位都是 $ \frac{1}{3} $。
答案:×
(5) 两个数的最小公倍数可能等于这两个数中的较大者,例如2和4的最小公倍数是4,并不比两个数都大。
答案:×
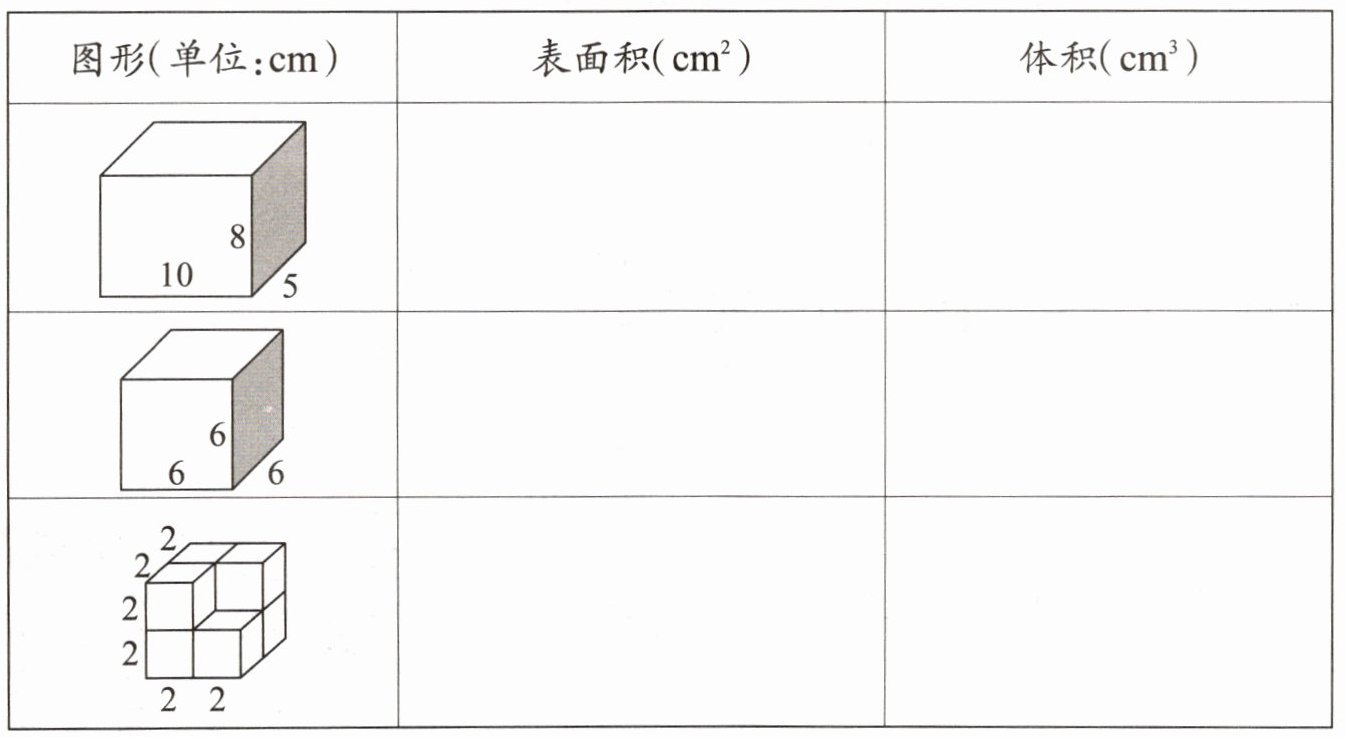
3 填写下表。

答案:
第一个图形为长方体:
表面积:
$S = 2 × (10 × 5 + 10 × 8 + 5 × 8)= 2 × (50 + 80 + 40) = 2 × 170 = 340$($cm^2$)。
体积:
$V = 10 × 5 × 8 = 400$($cm^3$)。
第二个图形为正方体:
表面积:
$S = 6 × (6 × 6) = 6 × 36 = 216$($cm^2$)。
体积:
$V = 6 × 6 × 6 = 216$($cm^3$)。
第三个图形为正方体,由$8$个小正方体组成:
表面积:
$S =6×4×2+6×2×2= 48 + 24 = 72$($cm^2$)。
体积:
$V = 2 × 2 × 2 × 8 = 64$($cm^3$)。
填表如下:
| 图形(单位:cm) | 表面积($cm^2$) | 体积($cm^3$) |
| --- | --- | --- |
| 长$10$,宽$5$,高$8$的长方体 | 340 | 400 |
| 边长为$6$的正方体 | 216 | 216 |
| 由$8$个边长为$2$的小正方体组成的大正方体 | 72 | 64 |
表面积:
$S = 2 × (10 × 5 + 10 × 8 + 5 × 8)= 2 × (50 + 80 + 40) = 2 × 170 = 340$($cm^2$)。
体积:
$V = 10 × 5 × 8 = 400$($cm^3$)。
第二个图形为正方体:
表面积:
$S = 6 × (6 × 6) = 6 × 36 = 216$($cm^2$)。
体积:
$V = 6 × 6 × 6 = 216$($cm^3$)。
第三个图形为正方体,由$8$个小正方体组成:
表面积:
$S =6×4×2+6×2×2= 48 + 24 = 72$($cm^2$)。
体积:
$V = 2 × 2 × 2 × 8 = 64$($cm^3$)。
填表如下:
| 图形(单位:cm) | 表面积($cm^2$) | 体积($cm^3$) |
| --- | --- | --- |
| 长$10$,宽$5$,高$8$的长方体 | 340 | 400 |
| 边长为$6$的正方体 | 216 | 216 |
| 由$8$个边长为$2$的小正方体组成的大正方体 | 72 | 64 |
查看更多完整答案,请扫码查看


