《2025年暑假作业长江少年儿童出版社五年级数学》

4 一个无盖的长方体玻璃鱼缸,长8dm,宽6dm,高5dm,制作这个鱼缸至少需要多少平方分米的玻璃？

答案： 解析：本题考查长方体表面积的计算。由于鱼缸无盖，所以只需求出这个长方体除上表面之外的$5$个面的面积之和即可。
长方体的前、后两个面的面积相同，每个面的面积为长$×$高，即$8×5 = 40$（平方分米），两个面的面积为$2×40 = 80$（平方分米）。
长方体的左、右两个面的面积相同，每个面的面积为宽$×$高，即$6×5 = 30$（平方分米），两个面的面积为$2×30 = 60$（平方分米）。
长方体的下表面的面积为长$×$宽，即$8×6 = 48$（平方分米）。
将前、后、左、右、下这$5$个面的面积相加，可得鱼缸所需玻璃的总面积为$80 + 60 + 48 = 188$（平方分米）。
答案：$8×5×2 + 6×5×2 + 8×6 = 188$（平方分米）。
答：制作这个鱼缸至少需要$188$平方分米的玻璃。

5) 一个正方体木块的棱长总和是96cm,那么它的体积是多少？

答案： 解析：本题考查正方体的棱长总和与体积的关系。需要用到正方体的棱长总和公式和体积公式。首先，通过棱长总和求出单条棱的长度，然后利用这个长度计算正方体的体积。
答案：
正方体有12条棱，每条棱的长度相等。设正方体的棱长为a cm。
根据棱长总和公式：
$12a = 96$
$a = \frac{96}{12} = 8 \text{cm}$
正方体的体积公式为：
$V = a^3$
$V = 8^3 = 512 \text{cm}^3$
答：它的体积是512立方厘米。

6) 小华带的钱如果都买牛奶,还剩下1元；如果都买果汁,也剩1元。小华至少带了多少钱？

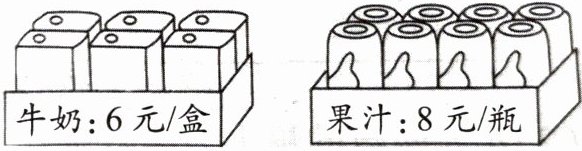
答案： 解析：本题考查最小公倍数的实际应用。
要求小华至少带了多少钱，需要先求出$6$和$8$的最小公倍数，
因为$6 = 2 × 3$，$8 = 2 × 2 × 2$，
所以$6$和$8$的最小公倍数为$2 × 2 × 2 × 3 = 24$。
小华带的钱比$6$和$8$的公倍数多$1$元，
那么小华至少带了$24 + 1 = 25$（元）。
答案：$25$元。

乐乐喝一瓶纯牛奶,分四次喝完。第一次喝了这瓶纯牛奶的$\frac{1}{3}$,然后加满水；第二次喝了$\frac{1}{6}$瓶,然后加满水；第三次喝了半瓶,又加满水；第四次一饮而尽。乐乐喝的纯牛奶多还是水多？为什么？

答案： 解析：本题考查利用分数计算实际问题。
乐乐最终喝完了所有的纯牛奶和水。需要计算他总共喝了多少纯牛奶和多少水，然后比较两者的量。
假设瓶子的容量为1。
乐乐喝的纯牛奶量：
乐乐第一次喝了$\frac{1}{3}$瓶纯牛奶。
乐乐第二次喝了$\frac{1}{6}$瓶纯牛奶（此时瓶内剩余纯牛奶为$\frac{2}{3} × \frac{5}{6}=\frac{5}{9}$，但此步骤我们只需考虑喝的量）。
乐乐第三次喝了半瓶纯牛奶（此时瓶内剩余纯牛奶为$\frac{5}{9} × \frac{1}{2}=\frac{5}{18}$，但同样只考虑喝的量）。
乐乐第四次一饮而尽，喝完了剩下的所有纯牛奶。
乐乐总共喝的纯牛奶量为：$\frac{1}{3} + \frac{1}{6} + \frac{1}{2} = 1$（瓶）。
乐乐喝的水的量：
乐乐第一次加了$\frac{1}{3}$瓶水。
乐乐第二次加了$\frac{1}{6}$瓶水。
乐乐第三次加了$\frac{1}{2}$瓶水。
乐乐第四次没有加水，因为他一饮而尽。
乐乐总共加的水的量为：$\frac{1}{3} + \frac{1}{6} + \frac{1}{2} = 1$（瓶）。
比较纯牛奶和水的量：
乐乐喝的纯牛奶总量为1瓶。
乐乐喝的水的总量也为1瓶。
因此，乐乐喝的纯牛奶和水一样多。
答案：乐乐喝的纯牛奶和水一样多，因为他总共喝了1瓶纯牛奶和1瓶水。