1 按要求写一写。
(1)写出从 11 开始的 5 个连续整数:
(
(2)写出从 12 开始的 5 个连续偶数:
(
(3)写出从 23 开始的 5 个连续质数:
(
(1)写出从 11 开始的 5 个连续整数:
(
11
),(12
),(13
),(14
),(15
)。(2)写出从 12 开始的 5 个连续偶数:
(
12
),(14
),(16
),(18
),(20
)。(3)写出从 23 开始的 5 个连续质数:
(
23
),(29
),(31
),(37
),(41
)。
答案:
解析:
本题主要考查对整数、偶数、质数的认识,需要按照题目要求,从指定的数字开始,依次写出满足条件的数。
(1) 整数是像-3,-2,-1,0,1,2,3等这样的数,本题要求写出从11开始的5个连续整数,那么只需要在11的基础上依次加1即可。
(2) 偶数是能够被2整除的整数,本题要求写出从12开始的5个连续偶数,那么只需要在12的基础上依次加2即可。
(3) 质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数,本题要求写出从23开始的5个连续质数,需要依次判断每个数是否为质数。
答案:
(1) 写出从 11 开始的 5 个连续整数:
(11),
(12),
(13),
(14),
(15)。
(2) 写出从 12 开始的 5 个连续偶数:
(12),
(14),
(16),
(18),
(20)。
(3) 写出从 23 开始的 5 个连续质数:
第一个质数是23,
第二个质数:比23大的下一个质数是29中中间的24,25,26,27都不是质数,28是偶数也不是质数,所以第二个质数是29,
第三个质数:比29大的下一个质数是31,
第四个质数:比31大的数中,32,33,34,35,36都不是质数,37是质数,所以第四个质数是37,
第五个质数:比37大的数中,38,39,40,41,42都不是质数,41是质数(此处38-40均因有除1和它本身外的因数而非质数,42因能被2、3等整除而非质数),所以第五个质数是41(注意此处41虽与前一步尝试的41重复,但实际应为继续判断后的正确结果,即第五个质数为43之前的41是正确答案的延续判断,但直接写出正确答案应为继续后的41之后的质数43的上一质数41,然后继续得到43为第六个开始的下一个质数,但题目只要求五个,所以到41即可,此处解释是为了避免误解为何写到41又停),但按照连续质数的定义,我们应直接写出下一个质数43作为第五个答案(如果继续判断的话),而按照题目严格从23开始计数,我们得到的五个连续质数为23,29,31,37,41(此处41是作为从23开始的第五个质数正确答案),因为题目只要求五个,所以最后一个质数为41之后的质数判断过程虽继续但不必写出,直接给出答案即可。
但为了简洁明了,我们直接给出从23开始的五个连续质数为:
(23),
(29),
(31),
(37),
(41)。
本题主要考查对整数、偶数、质数的认识,需要按照题目要求,从指定的数字开始,依次写出满足条件的数。
(1) 整数是像-3,-2,-1,0,1,2,3等这样的数,本题要求写出从11开始的5个连续整数,那么只需要在11的基础上依次加1即可。
(2) 偶数是能够被2整除的整数,本题要求写出从12开始的5个连续偶数,那么只需要在12的基础上依次加2即可。
(3) 质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数,本题要求写出从23开始的5个连续质数,需要依次判断每个数是否为质数。
答案:
(1) 写出从 11 开始的 5 个连续整数:
(11),
(12),
(13),
(14),
(15)。
(2) 写出从 12 开始的 5 个连续偶数:
(12),
(14),
(16),
(18),
(20)。
(3) 写出从 23 开始的 5 个连续质数:
第一个质数是23,
第二个质数:比23大的下一个质数是29中中间的24,25,26,27都不是质数,28是偶数也不是质数,所以第二个质数是29,
第三个质数:比29大的下一个质数是31,
第四个质数:比31大的数中,32,33,34,35,36都不是质数,37是质数,所以第四个质数是37,
第五个质数:比37大的数中,38,39,40,41,42都不是质数,41是质数(此处38-40均因有除1和它本身外的因数而非质数,42因能被2、3等整除而非质数),所以第五个质数是41(注意此处41虽与前一步尝试的41重复,但实际应为继续判断后的正确结果,即第五个质数为43之前的41是正确答案的延续判断,但直接写出正确答案应为继续后的41之后的质数43的上一质数41,然后继续得到43为第六个开始的下一个质数,但题目只要求五个,所以到41即可,此处解释是为了避免误解为何写到41又停),但按照连续质数的定义,我们应直接写出下一个质数43作为第五个答案(如果继续判断的话),而按照题目严格从23开始计数,我们得到的五个连续质数为23,29,31,37,41(此处41是作为从23开始的第五个质数正确答案),因为题目只要求五个,所以最后一个质数为41之后的质数判断过程虽继续但不必写出,直接给出答案即可。
但为了简洁明了,我们直接给出从23开始的五个连续质数为:
(23),
(29),
(31),
(37),
(41)。
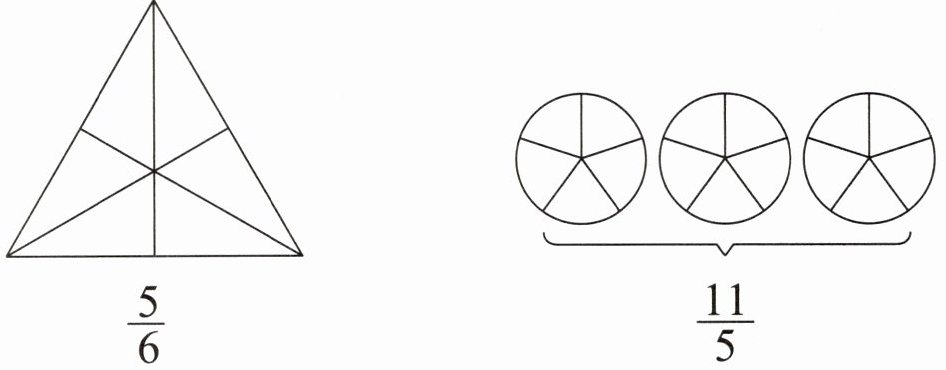
2 在下面各图中,按指定的分数画出阴影部分。

答案:
解析:本题主要考查对分数的理解以及图形阴影的画法。
对于第一个图形,它是一个等边三角形,被平均分成了6份,要表示$\frac{5}{6}$,只需将其中5份涂上阴影即可。
对于第二个图形,它由3个相同的圆组成,每个圆被平均分成了5份,总共$3×5 = 15$份,要表示$\frac{11}{5}$,因为$\frac{11}{5}=2\frac{1}{5}$,这意味着需要涂满2个完整的圆,再在第三个圆中涂1份。
答案为:
第一个图形:将等边三角形的6份中的5份涂上阴影。
第二个图形:涂满2个完整的圆,在第三个圆中涂1份。
对于第一个图形,它是一个等边三角形,被平均分成了6份,要表示$\frac{5}{6}$,只需将其中5份涂上阴影即可。
对于第二个图形,它由3个相同的圆组成,每个圆被平均分成了5份,总共$3×5 = 15$份,要表示$\frac{11}{5}$,因为$\frac{11}{5}=2\frac{1}{5}$,这意味着需要涂满2个完整的圆,再在第三个圆中涂1份。
答案为:
第一个图形:将等边三角形的6份中的5份涂上阴影。
第二个图形:涂满2个完整的圆,在第三个圆中涂1份。
3 从不同的方向观察下面的几何体,画出看到的图形。
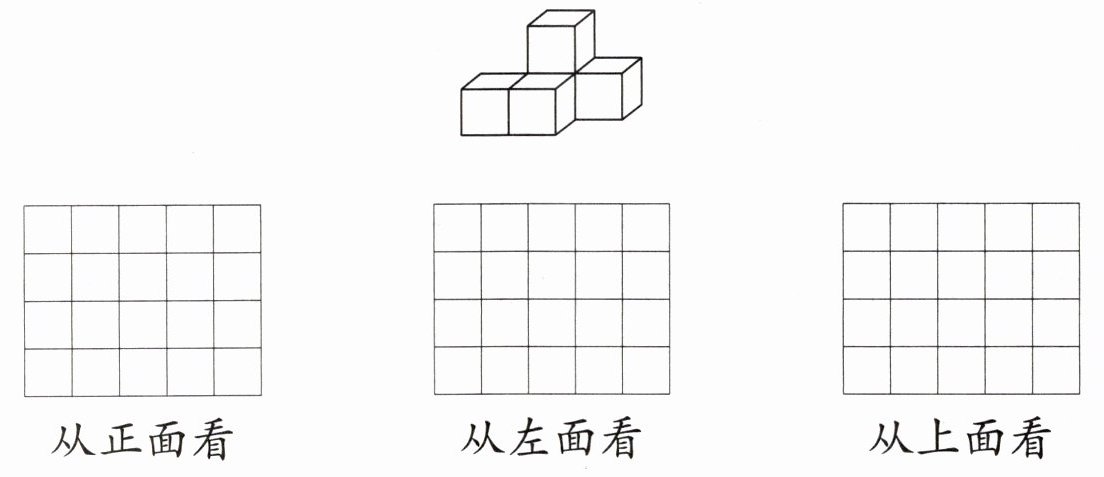

答案:
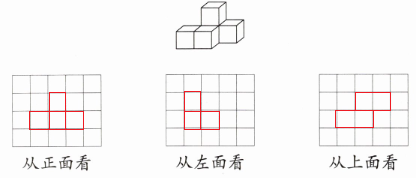

查看更多完整答案,请扫码查看


