3) 看图填一填。
从6:00到9:00,时针沿顺时针方向旋转了(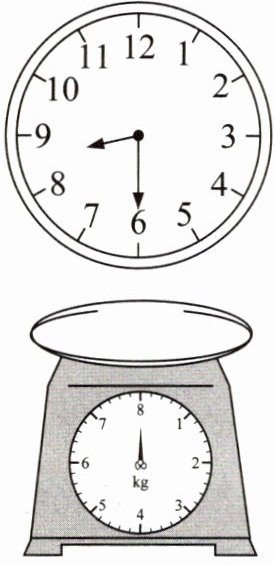
放上(
从6:00到9:00,时针沿顺时针方向旋转了(
90
)°;从3:00到12:00,时针沿顺时针方向旋转了(270
)°。
放上(
1
)kg物品可以使指针沿顺时针方向旋转90°。
答案:
解析:本题主要考查时钟的角度问题以及利用比例关系解决实际问题。对于时钟时针旋转角度的问题,需要知道时钟一圈为$360^{\circ}$,共$12$个大格,每个大格代表的角度是$360÷12 = 30^{\circ}$。从$6:00$到$9:00$,时针走了$9 - 6 = 3$个大格,所以旋转的角度是$3×30^{\circ}= 90^{\circ}$;从$3:00$到$12:00$,时针走了$12 - 3 = 9$个大格,旋转的角度是$9×30^{\circ}= 270^{\circ}$。对于放物品使指针旋转$90^{\circ}$的问题,从图中可知放$2kg$物品时指针旋转了$180^{\circ}$,设放$x kg$物品可以使指针沿顺时针方向旋转$90^{\circ}$,由于指针旋转角度与物品重量成正比例关系,则可列出比例式$2:180 = x:90$,通过解比例可求出$x$的值。
答案:从$6:00$到$9:00$,时针沿顺时针方向旋转的度数为:
$(9 - 6)×30^{\circ}= 90^{\circ}$;
从$3:00$到$12:00$,时针沿顺时针方向旋转的度数为:
$(12 - 3)×30^{\circ}= 270^{\circ}$;
设放$x kg$物品可以使指针沿顺时针方向旋转$90^{\circ}$。
因为放$2kg$物品时指针旋转了$180^{\circ}$,根据正比例关系可得:
$2:180 = x:90$,
$180x = 2×90$,
$180x = 180$,
$x = 1$。
故答案依次为:$90$;$270$;$1$。
答案:从$6:00$到$9:00$,时针沿顺时针方向旋转的度数为:
$(9 - 6)×30^{\circ}= 90^{\circ}$;
从$3:00$到$12:00$,时针沿顺时针方向旋转的度数为:
$(12 - 3)×30^{\circ}= 270^{\circ}$;
设放$x kg$物品可以使指针沿顺时针方向旋转$90^{\circ}$。
因为放$2kg$物品时指针旋转了$180^{\circ}$,根据正比例关系可得:
$2:180 = x:90$,
$180x = 2×90$,
$180x = 180$,
$x = 1$。
故答案依次为:$90$;$270$;$1$。
4) 某市2路公共汽车每6分钟发一次车,5路公共汽车每10分钟发一次。上午6时2路公共汽车和5路公共汽车同时发车,到中午12时,这两路公共汽车一共有多少次同时发车?
答案:
解析:
题目考查的是最小公倍数和时间段计算的知识点。
首先,需要找到6和10的最小公倍数,以确定两路公共汽车同时发车的频率。
其次,需要计算从上午6时到中午12时的时间总长度。
最后,将时间总长度除以两车同时发车的频率,再加上初始的同时发车次数(1次),即可得到总的同时发车次数。
答案:
首先,找到6和10的最小公倍数。
6的质因数分解为$2 × 3$,
10的质因数分解为$2 × 5$。
因此,6和10的最小公倍数为$2 × 3 × 5 = 30$。
这意味着每30分钟,两路公共汽车会同时发车一次。
接下来,计算从上午6时到中午12时的时间总长度。
时间总长度为$12 - 6 = 6(小时)$,
换算成分钟为$6 × 60 = 360(分钟)$。
然后,将时间总长度除以两车同时发车的频率,
即$360 ÷ 30 = 12(次)$。
但是,我们还需要加上初始的同时发车次数(1次),
所以总的同时发车次数为$12 + 1 = 13(次)$。
所以,从上午6时到中午12时,这两路公共汽车一共有13次同时发车。
题目考查的是最小公倍数和时间段计算的知识点。
首先,需要找到6和10的最小公倍数,以确定两路公共汽车同时发车的频率。
其次,需要计算从上午6时到中午12时的时间总长度。
最后,将时间总长度除以两车同时发车的频率,再加上初始的同时发车次数(1次),即可得到总的同时发车次数。
答案:
首先,找到6和10的最小公倍数。
6的质因数分解为$2 × 3$,
10的质因数分解为$2 × 5$。
因此,6和10的最小公倍数为$2 × 3 × 5 = 30$。
这意味着每30分钟,两路公共汽车会同时发车一次。
接下来,计算从上午6时到中午12时的时间总长度。
时间总长度为$12 - 6 = 6(小时)$,
换算成分钟为$6 × 60 = 360(分钟)$。
然后,将时间总长度除以两车同时发车的频率,
即$360 ÷ 30 = 12(次)$。
但是,我们还需要加上初始的同时发车次数(1次),
所以总的同时发车次数为$12 + 1 = 13(次)$。
所以,从上午6时到中午12时,这两路公共汽车一共有13次同时发车。
一个长方体的长是16cm,宽和高的厘米数均为质数。它的正面和上面的面积之和为$240cm^2。$
(1)这个长方体的体积是多少?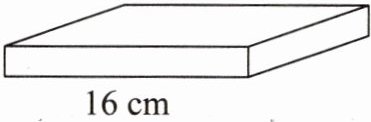
(2)这个长方体的表面积是多少?
(1)这个长方体的体积是多少?

(2)这个长方体的表面积是多少?
答案:
(1)设长方体的宽为$b$cm,高为$h$cm,$b$、$h$为质数。
正面面积为$16h$,上面面积为$16b$,由题意得:
$16b + 16h=240$
$16(b + h)=240$
$b + h=15$
小于15的质数有2,3,5,7,11,13。
其中$2 + 13=15$,$13 + 2=15$,$b$、$h$为质数,所以宽和高为2cm和13cm。
体积$V=16×2×13=416(cm^3)$
(2)表面积$S=2(16×2 + 16×13 + 2×13)$
$=2(32 + 208 + 26)$
$=2×266=532(cm^2)$
(1)416cm³
(2)532cm²
(1)设长方体的宽为$b$cm,高为$h$cm,$b$、$h$为质数。
正面面积为$16h$,上面面积为$16b$,由题意得:
$16b + 16h=240$
$16(b + h)=240$
$b + h=15$
小于15的质数有2,3,5,7,11,13。
其中$2 + 13=15$,$13 + 2=15$,$b$、$h$为质数,所以宽和高为2cm和13cm。
体积$V=16×2×13=416(cm^3)$
(2)表面积$S=2(16×2 + 16×13 + 2×13)$
$=2(32 + 208 + 26)$
$=2×266=532(cm^2)$
(1)416cm³
(2)532cm²
查看更多完整答案,请扫码查看


