(1)$\frac {5}{6}$的分数单位是(
$\frac{1}{6}$
)。它有(5
)个这样的分数单位。
答案:
解析:
一个分数的分数单位是其分母分之一。对于$\frac{5}{6}$,其分母是6,所以分数单位是$\frac{1}{6}$。
$\frac{5}{6}$可以看作是5个$\frac{1}{6}$相加,即:
$\frac{5}{6} = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6}$
所以,$\frac{5}{6}$有5个这样的分数单位。
答案:
$\frac {5}{6}$的分数单位是($\frac{1}{6}$)。它有
(5)个这样的分数单位。
一个分数的分数单位是其分母分之一。对于$\frac{5}{6}$,其分母是6,所以分数单位是$\frac{1}{6}$。
$\frac{5}{6}$可以看作是5个$\frac{1}{6}$相加,即:
$\frac{5}{6} = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6}$
所以,$\frac{5}{6}$有5个这样的分数单位。
答案:
$\frac {5}{6}$的分数单位是($\frac{1}{6}$)。它有
(5)个这样的分数单位。
(2)一个真分数,它的分母是最小的质数和最小的合数的积,这个真分数最大是$\frac {
7
}{8
}$。
答案:
解析:
首先,我们需要明确题目中的关键信息:
1. 这是一个真分数,即分子小于分母。
2. 分母是最小的质数和最小的合数的积。
接下来,我们根据这些信息进行计算:
1. 最小的质数是2,最小的合数是4。
2. 它们的积是$2×4=8$,所以分母是8。
3. 由于这是一个真分数,所以分子必须小于分母,即分子小于8。
4. 要使真分数最大,分子应该取最大值,即7(因为8-1=7,分子必须小于分母)。
所以,这个真分数最大是$\frac{7}{8}$。
答案:$\frac{7}{8}$,即这个真分数最大是$\frac {7}{8}$。
首先,我们需要明确题目中的关键信息:
1. 这是一个真分数,即分子小于分母。
2. 分母是最小的质数和最小的合数的积。
接下来,我们根据这些信息进行计算:
1. 最小的质数是2,最小的合数是4。
2. 它们的积是$2×4=8$,所以分母是8。
3. 由于这是一个真分数,所以分子必须小于分母,即分子小于8。
4. 要使真分数最大,分子应该取最大值,即7(因为8-1=7,分子必须小于分母)。
所以,这个真分数最大是$\frac{7}{8}$。
答案:$\frac{7}{8}$,即这个真分数最大是$\frac {7}{8}$。
(3)在$◯$里填上“>”“<”或“=”。
$\frac {5}{6}◯$
$\frac {5}{6}◯$
>
$\frac {4}{5}$ $\frac {1}{2}◯$<
$\frac {5}{9}$ $\frac {7}{8}◯$<
$\frac {8}{7}$ $0.8◯$>
$\frac {3}{5}$
答案:
解析:
题目考查分数的大小比较。对于分母不同的分数,需要找到公分母或者通过其他方法(如交叉相乘)来比较大小。对于分数与小数之间的比较,需要将分数转化为小数或者将小数转化为分数后进行比较。
答案:
$\frac{5}{6} > \frac{4}{5}$,因为交叉相乘得 $5 × 5 = 25$,$6 × 4 = 24$,$25 > 24$;
$\frac{1}{2} < \frac{5}{9}$,因为交叉相乘得 $1 × 9 = 9$,$2 × 5 = 10$,$9 < 10$;
$\frac{7}{8} < \frac{8}{7}$,因为 $\frac{7}{8} < 1$ 而 $\frac{8}{7} > 1$;
$0.8 > \frac{3}{5}$,因为 $\frac{3}{5} = 0.6$,$0.8 > 0.6$。
所以,$◯$里分别填:$>$,$<$,$<$,$>$。
题目考查分数的大小比较。对于分母不同的分数,需要找到公分母或者通过其他方法(如交叉相乘)来比较大小。对于分数与小数之间的比较,需要将分数转化为小数或者将小数转化为分数后进行比较。
答案:
$\frac{5}{6} > \frac{4}{5}$,因为交叉相乘得 $5 × 5 = 25$,$6 × 4 = 24$,$25 > 24$;
$\frac{1}{2} < \frac{5}{9}$,因为交叉相乘得 $1 × 9 = 9$,$2 × 5 = 10$,$9 < 10$;
$\frac{7}{8} < \frac{8}{7}$,因为 $\frac{7}{8} < 1$ 而 $\frac{8}{7} > 1$;
$0.8 > \frac{3}{5}$,因为 $\frac{3}{5} = 0.6$,$0.8 > 0.6$。
所以,$◯$里分别填:$>$,$<$,$<$,$>$。
(4)$1= \frac {(
10
)}{10}$ $2\frac {1}{3}= \frac {(7
)}{3}$ $\frac {19}{7}= (2
)\frac {(5
)}{7}$
答案:
解析:
第一个空,将整数1转换为分母为10的分数,即$\frac{10}{10}$,所以括号内应填10。
第二个空,将带分数$2\frac{1}{3}$转换为假分数,即$2 × 3 + 1 = 7$,再除以分母3,得到$\frac{7}{3}$,所以括号内应填7。
第三个和第四个空,将假分数$\frac{19}{7}$转换为带分数,19除以7得到商2余5,所以转换为带分数是$2\frac{5}{7}$,因此括号内应分别填2和5。
答案:
(4)$1= \frac {(10)}{10}$,$2\frac {1}{3}= \frac {(7)}{3}$,$\frac {19}{7}= (2)\frac {(5)}{7}$。
第一个空,将整数1转换为分母为10的分数,即$\frac{10}{10}$,所以括号内应填10。
第二个空,将带分数$2\frac{1}{3}$转换为假分数,即$2 × 3 + 1 = 7$,再除以分母3,得到$\frac{7}{3}$,所以括号内应填7。
第三个和第四个空,将假分数$\frac{19}{7}$转换为带分数,19除以7得到商2余5,所以转换为带分数是$2\frac{5}{7}$,因此括号内应分别填2和5。
答案:
(4)$1= \frac {(10)}{10}$,$2\frac {1}{3}= \frac {(7)}{3}$,$\frac {19}{7}= (2)\frac {(5)}{7}$。
(5)18的因数有
1,2,3,6,9,18
,24的因数有1,2,3,4,6,8,12,24
,18和24的公因数有1,2,3,6
,18和24的最大公因数是6
。
答案:
解析:本题主要考查因数、公因数和最大公因数的概念及求解方法。需要分别找出$18$和$24$的因数,再找出它们的公因数和最大公因数。
答案:
$1$,$2$,$3$,$6$,$9$,$18$;
$1$,$2$,$3$,$4$,$6$,$8$,$12$,$24$;
$1$,$2$,$3$,$6$;
$6$。
答案:
$1$,$2$,$3$,$6$,$9$,$18$;
$1$,$2$,$3$,$4$,$6$,$8$,$12$,$24$;
$1$,$2$,$3$,$6$;
$6$。
(6)若$A= 2×3×3×5,B= 2×2×3×5$,那么A和B的最大公因数是(
30
),A和B的最小公倍数是(180
)。
答案:
解析:本题主要考查最大公因数和最小公倍数的求法。
首先求A和B的最大公因数:
最大公因数是两个或多个整数共有的最大的因数。
为了找到A和B的最大公因数,需要找出它们共有的因数,并从中选择最大的。
观察A和B的质因数分解式,可以看到它们共有的质因数是2、3和5。
其中,2的最高次幂是1,3的最高次幂是1,5的最高次幂也是1。
因此,A和B的最大公因数是 $2^1 × 3^1 × 5^1 = 30$。
接下来求A和B的最小公倍数:
最小公倍数是两个或多个整数的公倍数中最小的一个。
为了找到A和B的最小公倍数,需要将它们所有的质因数(包括共有的和各自独有的)全部乘起来,并且每个质因数的幂次要取它在各个数中出现次数的最大值。
A和B的质因数包括2、3和5。其中,2在A中的幂次是1,在B中的幂次是2,所以取最大的幂次2;
3在A和B中的幂次都是1,所以取1;
5在A和B中的幂次都是1,所以也取1。
另外,A中还有一个独有的质因数3(因为A有两个3作为因数,而B只有一个),所以也需要将它乘进去。
因此,A和B的最小公倍数是 $2^2 × 3^2 × 5^1 = 180$。
答案:30;180。
首先求A和B的最大公因数:
最大公因数是两个或多个整数共有的最大的因数。
为了找到A和B的最大公因数,需要找出它们共有的因数,并从中选择最大的。
观察A和B的质因数分解式,可以看到它们共有的质因数是2、3和5。
其中,2的最高次幂是1,3的最高次幂是1,5的最高次幂也是1。
因此,A和B的最大公因数是 $2^1 × 3^1 × 5^1 = 30$。
接下来求A和B的最小公倍数:
最小公倍数是两个或多个整数的公倍数中最小的一个。
为了找到A和B的最小公倍数,需要将它们所有的质因数(包括共有的和各自独有的)全部乘起来,并且每个质因数的幂次要取它在各个数中出现次数的最大值。
A和B的质因数包括2、3和5。其中,2在A中的幂次是1,在B中的幂次是2,所以取最大的幂次2;
3在A和B中的幂次都是1,所以取1;
5在A和B中的幂次都是1,所以也取1。
另外,A中还有一个独有的质因数3(因为A有两个3作为因数,而B只有一个),所以也需要将它乘进去。
因此,A和B的最小公倍数是 $2^2 × 3^2 × 5^1 = 180$。
答案:30;180。
(7)在$\frac {1}{2}$、$\frac {16}{24}$、$\frac {34}{51}$、$\frac {15}{13}$、$\frac {31}{32}$中,最简分数有
$\frac{1}{2}$,$\frac{15}{13}$,$\frac{31}{32}$
。
答案:
解析:最简分数是分子和分母只有公因数1的分数。
$\frac{1}{2}$的分子和分母只有公因数1,所以它是最简分数。
$\frac{16}{24}$的分子和分母有公因数2、4、8等,所以它不是最简分数,可以化简为$\frac{2}{3}$。
$\frac{34}{51}$的分子和分母有公因数17,所以它不是最简分数,可以化简为$\frac{2}{3}$。
$\frac{15}{13}$的分子和分母只有公因数1,所以它是最简分数。
$\frac{31}{32}$的分子和分母只有公因数1,所以它是最简分数。
答案:$\frac{1}{2}$,$\frac{15}{13}$,$\frac{31}{32}$。
$\frac{1}{2}$的分子和分母只有公因数1,所以它是最简分数。
$\frac{16}{24}$的分子和分母有公因数2、4、8等,所以它不是最简分数,可以化简为$\frac{2}{3}$。
$\frac{34}{51}$的分子和分母有公因数17,所以它不是最简分数,可以化简为$\frac{2}{3}$。
$\frac{15}{13}$的分子和分母只有公因数1,所以它是最简分数。
$\frac{31}{32}$的分子和分母只有公因数1,所以它是最简分数。
答案:$\frac{1}{2}$,$\frac{15}{13}$,$\frac{31}{32}$。
(8)化简一个分数时,用2约了两次,用3约了一次,得$\frac {4}{5}$。原来的分数是$\frac {(
48
)}{(60
)}$。
答案:
解析:
本题考查的是分数的基本性质。
即分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
为了找到原来的分数,需要将分子和分母都乘以约定的数。
具体地,用2约了两次,用3约了一次,所以需要将分子和分母都乘以$2 × 2 × 3$。
对于分子:
$4 × 2 × 2 × 3 = 48$。
对于分母:
$5 × 2 × 2 × 3 = 60$。
所以,原来的分数是 $\frac{48}{60}$。
答案为:48;60。
本题考查的是分数的基本性质。
即分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
为了找到原来的分数,需要将分子和分母都乘以约定的数。
具体地,用2约了两次,用3约了一次,所以需要将分子和分母都乘以$2 × 2 × 3$。
对于分子:
$4 × 2 × 2 × 3 = 48$。
对于分母:
$5 × 2 × 2 × 3 = 60$。
所以,原来的分数是 $\frac{48}{60}$。
答案为:48;60。
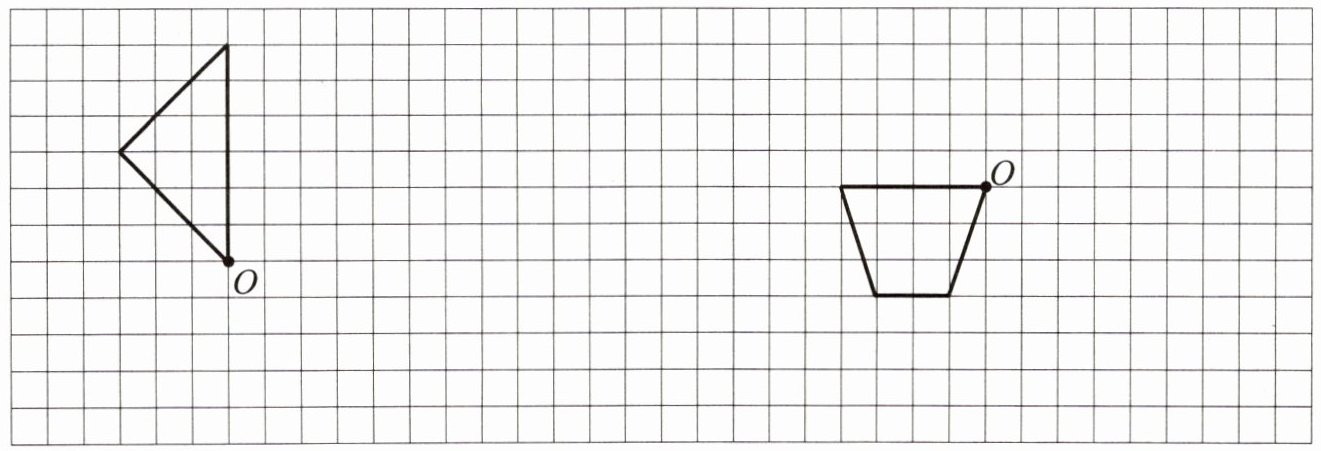
2 分别画出三角形绕点O逆时针旋转$90^{\circ }$、梯形绕点O顺时针旋转$90^{\circ }$后的图形。

答案:
(注:因无法直接绘制图形,此处仅描述作图步骤,实际答题需在答题卡给定网格中按步骤画出图形。)
1. 三角形绕点O逆时针旋转90°:
确定三角形各顶点(除O外)与点O的水平和垂直距离。
每个顶点绕O逆时针旋转90°:原坐标(x,y)变为(-y,x)(以O为原点)。
连接旋转后各顶点及点O,得到旋转后三角形。
2. 梯形绕点O顺时针旋转90°:
确定梯形各顶点(除O外)与点O的水平和垂直距离。
每个顶点绕O顺时针旋转90°:原坐标(x,y)变为(y,-x)(以O为原点)。
连接旋转后各顶点及点O,得到旋转后梯形。
(注:实际答题需在答题卡网格中准确绘制出上述两个旋转后的图形。)
1. 三角形绕点O逆时针旋转90°:
确定三角形各顶点(除O外)与点O的水平和垂直距离。
每个顶点绕O逆时针旋转90°:原坐标(x,y)变为(-y,x)(以O为原点)。
连接旋转后各顶点及点O,得到旋转后三角形。
2. 梯形绕点O顺时针旋转90°:
确定梯形各顶点(除O外)与点O的水平和垂直距离。
每个顶点绕O顺时针旋转90°:原坐标(x,y)变为(y,-x)(以O为原点)。
连接旋转后各顶点及点O,得到旋转后梯形。
(注:实际答题需在答题卡网格中准确绘制出上述两个旋转后的图形。)
查看更多完整答案,请扫码查看


