《2025年暑假作业长江少年儿童出版社五年级数学》

3 一个正方体容器,从里面量棱长是20cm,装满水后,再将它里面的水倒入容积是250mL的玻璃瓶里,每瓶都倒满,可以倒多少瓶?

答案： 解析：本题考查正方体体积的计算以及单位换算。
首先计算正方体容器的体积：
正方体的体积公式是$V = a^{3}$，其中a是正方体的棱长。
给定正方体的棱长为20cm，所以正方体的体积为：
$V = 20^{3} = 8000 (cm^{3})$；
进行单位换算：
题目中需要将水的体积从立方厘米转换为毫升。
由于$1 cm^{3} = 1 mL$，所以8000 $cm^{3}$ = 8000 mL。
计算可以倒满的玻璃瓶数量：
给定每瓶玻璃瓶的容积为250mL，所以可以倒满的玻璃瓶数量为：
$8000÷ 250 = 32$ (瓶)。
答案：可以倒32瓶。

4 把一张长45cm、宽30cm的长方形纸裁成同样大小、面积尽可能大的正方形纸,且纸没有剩余,至少可以裁出多少张正方形纸?

答案： 解析：本题考查最大公约数的应用。
首先，找到$45$和$30$的最大公约数。
$45$的因数有：$1, 3, 5, 9, 15, 45$，
$30$的因数有：$1, 2, 3, 5, 6, 10, 15, 30$，
所以，$45$和$30$的最大公约数是$15$。
因此，最大的正方形边长为$15cm$。
然后，计算可以裁出多少张这样的正方形纸。
长方形纸的面积是 $45 × 30 = 1350 ({cm}^{2})$，
每个正方形的面积是 $15 × 15 = 225 ({cm}^{2})$，
所以，可以裁出的正方形数量是 $\frac{1350}{225} = 6（张）$。
答案：至少可以裁出$6$张正方形纸。

5 小方和小林同时从甲、乙两地出发,相向而行。当小方走了全程的$\frac {1}{2}$时,小林走了全程的$\frac {2}{3}$。他们相遇了吗? 你是怎样判断的?

答案： 解析：
本题考查对分数的理解和相遇问题的判断。
两人同时出发，相向而行，那么他们走过的路程之和就是甲乙两地的总路程。
当小方走了全程的$\frac {1}{2}$时，也就是走了全程的一半，小林走了全程的$\frac {2}{3}$，那么两人走过的路程之和超过了全程，即：
$\frac {1}{2}+\frac {2}{3}=\frac{3}{6}+\frac{4}{6}=\frac{7}{6}$
$\frac{7}{6} \gt 1$
由于他们走过的路程之和超过了甲乙两地的总路程，所以他们已经相遇过，并且小林走过的路程还超出了全程的$\frac{1}{6}$。
答案：
他们相遇了。因为小方走了全程的$\frac {1}{2}$，小林走了全程的$\frac {2}{3}$，他们两人走过的路程之和为$\frac{7}{6}$，超过了全程，所以他们相遇了。

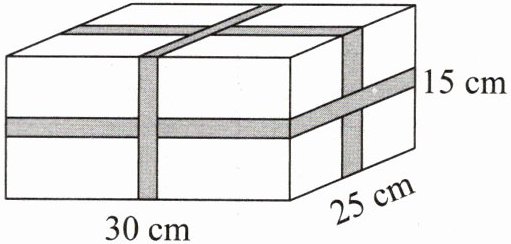
为了物品的安全,快递公司在收件时给一个长方体盒子绑上胶带(如图)。一共需要多长的胶带? (接头处忽略不计)

答案： 解：长方体盒子的长为30cm，宽为25cm，高为15cm。
胶带长度为两个长、两个宽和四个高的总和，即：
$2×30 + 2×25 + 4×15$
$=60 + 50 + 60$
$=170$（cm）
答：一共需要170cm长的胶带。