(1) 长方体有
6
个面,且长方体的面一般是长方
形。长方体也可能有2
个相对的面是正方形,长方体相对的面的面积相等
。
答案:
解析:本题考查长方体的基本特征。长方体是一个三维的几何图形,它有6个面、12条棱和8个顶点。一般情况下,它的6个面都是长方形,但也可能有2个相对的面是正方形。长方体相对的面的面积相等。
答案:6,长方,2,相等。
答案:6,长方,2,相等。
(2) 右图是一个长方体顶点处的3条棱(单位:cm)。那么,这个长方体的棱长总和是(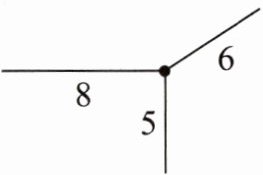
76
)cm,前面的面积是(48
)$cm^{2}$, 右面的面积是(30
)$cm^{2}$。
答案:
解析:本题主要考查长方体的棱长总和以及不同面的面积计算。需要运用长方体棱长总和公式以及长方形面积公式来求解。
棱长总和:长方体棱长总和 =(长 + 宽 + 高)× 4。
前面的面积:前面的面积 = 长×高。
右面的面积:右面的面积 = 宽×高。
从图中可知长方体的长为$8cm$、宽为$5cm$、高为$6cm$。
棱长总和:$(8 + 5 + 6)× 4 = 76$(cm)。
前面的面积:$8× 6 = 48$($cm^{2}$)。
右面的面积:$5× 6 = 30$($cm^{2}$)。
答案:76;48;30。
棱长总和:长方体棱长总和 =(长 + 宽 + 高)× 4。
前面的面积:前面的面积 = 长×高。
右面的面积:右面的面积 = 宽×高。
从图中可知长方体的长为$8cm$、宽为$5cm$、高为$6cm$。
棱长总和:$(8 + 5 + 6)× 4 = 76$(cm)。
前面的面积:$8× 6 = 48$($cm^{2}$)。
右面的面积:$5× 6 = 30$($cm^{2}$)。
答案:76;48;30。
(3) 一个长85cm、宽42cm、高63cm的长方体纸箱最多能装下(
24
)个棱长为20cm的正方体玻璃缸。
答案:
解析:本题考查长方体体积和正方体体积的计算和实际应用。
长方体体积公式:$V = a × b × h$,其中a、b、h分别为长方体的长、宽、高。
正方体体积公式:$V = a^{3}$,其中a为正方体的棱长。
首先,计算长方体纸箱的体积:
$V_{长方体} = 85 × 42 × 63 = 224910({cm}^{3})$
然后,计算正方体玻璃缸的体积:
$V_{正方体} = 20^{3} = 8000({cm}^{3})$
理论上,长方体纸箱最多能装下的正方体玻璃缸的数量为长方体纸箱的体积除以正方体玻璃缸的体积:
$N_{理论} = \frac{V_{长方体}}{V_{正方体}} = \frac{224910}{8000} \approx 28.11$
由于不能将正方体玻璃缸切割,所以实际能装下的数量应该是理论数量的整数部分,即28个。但这里需要考虑长方体的实际尺寸和正方体的尺寸关系。
沿着长方体的长度方向,可以放置 $\lfloor \frac{85}{20} \rfloor = 4$ 个正方体。
沿着长方体的宽度方向,可以放置 $\lfloor \frac{42}{20} \rfloor = 2$ 个正方体。
沿着长方体的高度方向,可以放置 $\lfloor \frac{63}{20} \rfloor = 3$ 个正方体。
因此,实际可以放置的正方体数量为 $4 × 2 × 3 = 24$ 个。
答案:24个。
长方体体积公式:$V = a × b × h$,其中a、b、h分别为长方体的长、宽、高。
正方体体积公式:$V = a^{3}$,其中a为正方体的棱长。
首先,计算长方体纸箱的体积:
$V_{长方体} = 85 × 42 × 63 = 224910({cm}^{3})$
然后,计算正方体玻璃缸的体积:
$V_{正方体} = 20^{3} = 8000({cm}^{3})$
理论上,长方体纸箱最多能装下的正方体玻璃缸的数量为长方体纸箱的体积除以正方体玻璃缸的体积:
$N_{理论} = \frac{V_{长方体}}{V_{正方体}} = \frac{224910}{8000} \approx 28.11$
由于不能将正方体玻璃缸切割,所以实际能装下的数量应该是理论数量的整数部分,即28个。但这里需要考虑长方体的实际尺寸和正方体的尺寸关系。
沿着长方体的长度方向,可以放置 $\lfloor \frac{85}{20} \rfloor = 4$ 个正方体。
沿着长方体的宽度方向,可以放置 $\lfloor \frac{42}{20} \rfloor = 2$ 个正方体。
沿着长方体的高度方向,可以放置 $\lfloor \frac{63}{20} \rfloor = 3$ 个正方体。
因此,实际可以放置的正方体数量为 $4 × 2 × 3 = 24$ 个。
答案:24个。
(4) 一个正方体的棱长总和是60cm,它的体积是(
125
)$cm^{3}$, 表面积是(150
)$cm^{2}$。
答案:
解析:
首先,正方体有12条棱,且每条棱的长度相等。
由题意知正方体的棱长总和是60cm,所以单条棱的长度为:
$\text{棱长} = \frac{60}{12} = 5(cm)$
接下来,计算正方体的体积。
正方体的体积公式为:
$V = a^{3}$
其中,a为正方体的棱长。
代入a=5cm,得:
$V = 5^{3} = 125(cm^{3})$
再计算正方体的表面积。
正方体的表面积公式为:
$S = 6a^{2}$
代入a=5cm,得:
$S = 6 × 5^{2} = 150(cm^{2})$
答案:
一个正方体的棱长总和是60cm,它的体积是$125cm^{3}$,表面积是$150cm^{2}$。
首先,正方体有12条棱,且每条棱的长度相等。
由题意知正方体的棱长总和是60cm,所以单条棱的长度为:
$\text{棱长} = \frac{60}{12} = 5(cm)$
接下来,计算正方体的体积。
正方体的体积公式为:
$V = a^{3}$
其中,a为正方体的棱长。
代入a=5cm,得:
$V = 5^{3} = 125(cm^{3})$
再计算正方体的表面积。
正方体的表面积公式为:
$S = 6a^{2}$
代入a=5cm,得:
$S = 6 × 5^{2} = 150(cm^{2})$
答案:
一个正方体的棱长总和是60cm,它的体积是$125cm^{3}$,表面积是$150cm^{2}$。
(5) $0.76m^{3}=$
$360mL=$
$500mL=$
760
$dm^{3}$ $1200cm^{3}=$1.2
$dm^{3}$$360mL=$
0.36
$L$ $1.05L=$1050
$mL$$500mL=$
0.5
$dm^{3}$ $9.6L=$9600
$cm^{3}$
答案:
解析:本题考查的是体积单位和容积单位的换算。根据单位间的换算关系,我们可以得到以下答案。
答案:$760$;$1.2$;$0.36$;$1050$;$0.5$;$9600$。
答案:$760$;$1.2$;$0.36$;$1050$;$0.5$;$9600$。
2) 计算下面各题。
$\frac {5}{3}-(\frac {2}{5}+\frac {3}{10})$ $\frac {5}{6}-(\frac {4}{9}-\frac {1}{3})$
$\frac {4}{5}-\frac {4}{11}+\frac {1}{5}+\frac {7}{11}$ $\frac {3}{4}+\frac {6}{13}+\frac {7}{13}-\frac {1}{4}$
$\frac {5}{3}-(\frac {2}{5}+\frac {3}{10})$ $\frac {5}{6}-(\frac {4}{9}-\frac {1}{3})$
$\frac {4}{5}-\frac {4}{11}+\frac {1}{5}+\frac {7}{11}$ $\frac {3}{4}+\frac {6}{13}+\frac {7}{13}-\frac {1}{4}$
答案:
解析:
这些题目主要考查分数的加减运算,包括分数的通分、合并与简化。
对于带有括号的表达式,需要先计算括号内的部分;
对于多个分数相加减的表达式,可以通过加法交换律和结合律进行简化。
答案:
1. 计算 $\frac {5}{3}-(\frac {2}{5}+\frac {3}{10})$
$\;\;\;\; \frac {5}{3}-(\frac {2}{5}+\frac {3}{10})$
$=\frac {5}{3}-(\frac {4}{10}+\frac {3}{10})$
$=\frac {5}{3}-\frac {7}{10}$
$=\frac {50}{30}-\frac {21}{30}$
$=\frac {29}{30}$
2. 计算 $\frac {5}{6}-(\frac {4}{9}-\frac {1}{3})$
$\;\;\;\; \frac {5}{6}-(\frac {4}{9}-\frac {1}{3})$
$=\frac {5}{6}-(\frac {4}{9}-\frac {3}{9})$
$=\frac {5}{6}-\frac {1}{9}$
$=\frac {45}{54}-\frac {6}{54}$
$=\frac {39}{54}$
$=\frac {13}{18}$
3. 计算 $\frac {4}{5}-\frac {4}{11}+\frac {1}{5}+\frac {7}{11}$
$\;\;\;\; \frac {4}{5}-\frac {4}{11}+\frac {1}{5}+\frac {7}{11}$
$=(\frac {4}{5}+\frac {1}{5})+(\frac {7}{11}-\frac {4}{11})$
$=1+\frac {3}{11}$
$=\frac {14}{11}$
4. 计算 $\frac {3}{4}+\frac {6}{13}+\frac {7}{13}-\frac {1}{4}$
$\;\;\;\; \frac {3}{4}+\frac {6}{13}+\frac {7}{13}-\frac {1}{4}$
$=(\frac {3}{4}-\frac {1}{4})+(\frac {6}{13}+\frac {7}{13})$
$=\frac {1}{2}+1$
$=\frac {3}{2}$
这些题目主要考查分数的加减运算,包括分数的通分、合并与简化。
对于带有括号的表达式,需要先计算括号内的部分;
对于多个分数相加减的表达式,可以通过加法交换律和结合律进行简化。
答案:
1. 计算 $\frac {5}{3}-(\frac {2}{5}+\frac {3}{10})$
$\;\;\;\; \frac {5}{3}-(\frac {2}{5}+\frac {3}{10})$
$=\frac {5}{3}-(\frac {4}{10}+\frac {3}{10})$
$=\frac {5}{3}-\frac {7}{10}$
$=\frac {50}{30}-\frac {21}{30}$
$=\frac {29}{30}$
2. 计算 $\frac {5}{6}-(\frac {4}{9}-\frac {1}{3})$
$\;\;\;\; \frac {5}{6}-(\frac {4}{9}-\frac {1}{3})$
$=\frac {5}{6}-(\frac {4}{9}-\frac {3}{9})$
$=\frac {5}{6}-\frac {1}{9}$
$=\frac {45}{54}-\frac {6}{54}$
$=\frac {39}{54}$
$=\frac {13}{18}$
3. 计算 $\frac {4}{5}-\frac {4}{11}+\frac {1}{5}+\frac {7}{11}$
$\;\;\;\; \frac {4}{5}-\frac {4}{11}+\frac {1}{5}+\frac {7}{11}$
$=(\frac {4}{5}+\frac {1}{5})+(\frac {7}{11}-\frac {4}{11})$
$=1+\frac {3}{11}$
$=\frac {14}{11}$
4. 计算 $\frac {3}{4}+\frac {6}{13}+\frac {7}{13}-\frac {1}{4}$
$\;\;\;\; \frac {3}{4}+\frac {6}{13}+\frac {7}{13}-\frac {1}{4}$
$=(\frac {3}{4}-\frac {1}{4})+(\frac {6}{13}+\frac {7}{13})$
$=\frac {1}{2}+1$
$=\frac {3}{2}$
查看更多完整答案,请扫码查看


