《2025年全效学习学业评价方案九年级数学上册北师大版》

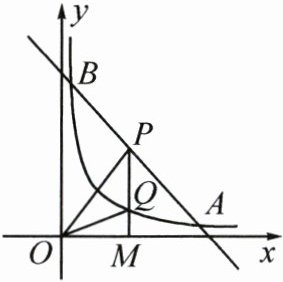
22. (12分)如图,一次函数$y_{1}=kx+b(k≠0)$与函数$y_{2}=\frac {m}{x}(x＞0)$的图象交于$A(4,1),B(\frac {1}{2},a)$两点.
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足$y_{1}-y_{2}＞0$时$x$的取值范围;
(3)点$P$在线段$AB$上,过点$P$作$x$轴的垂线,垂足为$M$,交函数$y_{2}$的图象于点$Q$,若$\triangle POQ$的面积为3,求点$P$的坐标.

答案： （1）反比例函数的表达式为 $ y_2 = \frac{4}{x} (x ＞ 0) $。一次函数的表达式为 $ y_1 = -2x + 9 $。
（2）$ \frac{1}{2} ＜ x ＜ 4 $
（3）点 P 的坐标为 $ (\frac{5}{2}, 4) $ 或 $ (2, 5) $。

23. (13分)如图,在平面直角坐标系中,一次函数$y=-x+1$与反比例函数$y=\frac {k}{x}$的图象在第四象限相交于点$A(2,-1)$,一次函数的图象与$x$轴相交于点$B$.
(1)求反比例函数的表达式及点$B$的坐标;
$ y = -\frac{2}{x} $，$ B(1, 0) $
(2)当一次函数值小于反比例函数值时,请直接写出$x$的取值范围是____;
$ -1 ＜ x ＜ 0 $ 或 $ x ＞ 2 $
(3)点$C$是第二象限内直线$AB$上的一个动点,过点$C$作$CD// x$轴,交反比例函数$y=\frac {k}{x}$的图象于点$D$,若以$O,B,C,D$为顶点的四边形为平行四边形,请直接写出点$C$的坐标.
$ C(1 - \sqrt{2}, \sqrt{2}) $ 或 $ (-\sqrt{3}, 1 + \sqrt{3}) $

答案： （1）$ y = -\frac{2}{x} $，$ B(1, 0) $。
（2）$ -1 ＜ x ＜ 0 $ 或 $ x ＞ 2 $
（3）$ C(1 - \sqrt{2}, \sqrt{2}) $ 或 $ (-\sqrt{3}, 1 + \sqrt{3}) $。